Finer geometry of planar self-affine sets
Affine iterated function systems

Let \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_2(\mathbb{R})^N\) be a tuple of invertible \(2 \times 2\)-matrices such that \(\|A_i\|<1\) for all \(i\). A tuple \(\Phi = (\varphi_1,\ldots,\varphi_N)\) of contractive invertible affine maps \(\varphi_i \colon \mathbb{R}^2 \to \mathbb{R}^2\), \(\varphi_i(x) = A_ix + t_i\), is called an affine iterated function system (IFS).
Theorem 1 (Hutchinson (1981)).
For every affine IFS \(\Phi\) there exists a unique non-empty compact set \(X \subset \mathbb{R}^2\) such that
\[X = \bigcup_{i=1}^N \varphi_i(X).\]
The set \(X\) is called self-affine. If \(A_i = \lambda_i O_i\) for some \(0<|\lambda_i|<1\)
and \(O_i \in O(2)\), then the set \(X\) is called self-similar.
Planar self-similar sets
The similarity dimension \(\dim_{\mathrm{sim}}(X)\) of a self-similar set \(X\)
is the unique \(s \ge 0\) for which \(\sum_{i=1}^N |\lambda_i|^s = 1\).
If \(\mathtt{i} = i_1 \cdots i_n \in I^* = \bigcup_{k=1}^\infty I^k\), where \(I = \{1,\ldots,N\}\), then we write
\(\varphi_\mathtt{i} = \varphi_{i_1} \circ \cdots \circ \varphi_{i_n}\), \(A_{\mathtt{i}} = A_{i_1} \cdots A_{i_n}\), and \(\lambda_\mathtt{i} = \lambda_{i_1} \cdots \lambda_{i_n}\). The similarity dimension is an upper bound for the Hausdorff dimension:
Lemma 2 (Hutchinson (1981)).
If \(X \subset \mathbb{R}^2\) is a self-similar set, then \(\dim_{\mathrm{H}}(X) \le \min\{2,\dim_{\mathrm{sim}}(X)\}\).
Proof. Since
\[\begin{equation*}
\mathcal{H}^s_\delta(X) \le \sum_{\mathtt{i} \in I^n} \mathrm{diam}(\varphi_\mathtt{i}(X))^s
= \mathrm{diam}(X)^s \sum_{\mathtt{i} \in I^n} |\lambda_\mathtt{i}|^s = \mathrm{diam}(X)^s \Bigl( \sum_{i=1}^N |\lambda_i|^s \Bigr)^n,
\end{equation*}\]
the claim holds. ■
A self-similar set satisfies the open set condition (OSC) if there exists an open set \(U \subset \mathbb{R}^2\) such that \(\varphi_i(U) \cap \varphi_j(U) = \emptyset\) for \(i \ne j\). A set \(X\) is Ahlfors \(s\)-regular if there exists a constant \(C \ge 1\) such that
\[C^{-1}r^s \le \mathcal{H}^s(X \cap B(x,r)) \le Cr^s\]
for all \(x \in X\) and \(0<r<\mathrm{diam}(X)\). If \(X\) is Ahlfors \(s\)-regular, then trivially \(\mathcal{H}^s(X)>0\).
Theorem 3 (Hutchinson (1981)).
If \(X \subset \mathbb{R}^2\) is a self-similar set satisfying the OSC and \(s = \dim_{\mathrm{sim}}(X)\), then \(X\) is Ahlfors \(s\)-regular. In particular, \(\mathcal{H}^s(X)>0\) and \(\dim_{\mathrm{H}}(X) = s\).
Proof. The equilibrium state \(\mu\) on \(X\) satisfies \(\mu(\varphi_\mathtt{i}(X))=|\lambda_\mathtt{i}|^s\),
where \(s = \dim_{\mathrm{sim}}(\Phi)\). Since
\[\mu(B(x,r)) \le \sum \mu(\varphi_\mathtt{i}(X)) = \sum |\lambda_\mathtt{i}|^s \le Mr^s,\]
where the sums are over all \(\mathtt{i}\) with \(\mathrm{diam}(\varphi_\mathtt{i}(X)) \approx r\) and
\(\varphi_\mathtt{i}(X) \cap B(x,r) \ne \emptyset\). By choosing the largest \(\varphi_\mathtt{i}(X)) \subset B(x,r)\),
we get the opposite inequality. Hence, \(\mu\) is equivalent to \(\mathcal{H}^s|_X\) and the claims follow. ■
These conditions have been since proven to be equivalent:
Theorem 4 (Bandt-Graf (1992), Falconer (1989), and Schief (1994)).
If \(X \subset \mathbb{R}^2\) is a self-similar set and \(s = \dim_{\mathrm{sim}}(X)\), then the following conditions are equivalent:
(1) \(X\) satisfies the OSC,
(2) \(X\) is Ahlfors \(s\)-regular,
(3) \(\mathcal{H}^s(X)>0\),
(4) there is \(\eta>0\) such that
\(|\varphi_\mathtt{i}-\varphi_\mathtt{j}| \ge \eta\mathrm{diam}(\varphi_\mathtt{i}(X))\)
for all \(\mathtt{i},\mathtt{j} \in I^*\) with \(\mathtt{i} \ne \mathtt{j}\).
In fact, any self-similar set \(X\) has finite measure, \(\mathcal{H}^s(X) < \infty\) for \(s = \dim_{\mathrm{H}}(X)\).
The Assouad dimension of a set \(X \subset \mathbb{R}^2\), denoted by \(\dim_{\mathrm{A}}(X)\), is the infimum of all \(s \ge 0\) satisfying the following: There exists a constant \(C \ge 1\) such that for every \(x \in X\) and \(0<r<R\) the set \(X \cap B(x,R)\) can be covered by at most \(C(R/r)^s\) balls of radius \(r\) centered at \(X\).
Analogously, the lower dimension of a set \(X \subset \mathbb{R}^2\), denoted by \(\dim_{\mathrm{L}}(X)\), is the supremum of all \(s \ge 0\) satisfying the following: There exists a constant \(c>0\) such that for every \(x \in X\) and
\(0 < r < R < \mathrm{diam}(X)\) covering the set \(X \cap B(x,R)\) requires at least \(c(r/R)^{-t}\) balls of radius \(r\) centered at \(X\).
It is straightforward to see that
\[\dim_{\mathrm{L}}(X) \le \dim_{\mathrm{H}}(X) \le \dim_{\mathrm{A}}(X)\]
for all \(X \subset \mathbb{R}^2\) and
\[\dim_{\mathrm{L}}(X) = \dim_{\mathrm{H}}(X) = \dim_{\mathrm{A}}(X)\]
for all Ahlfors regular \(X \subset \mathbb{R}^2\).
A self-similar set \(X\) satisfies the weak separation condition (WSC) if there is \(\eta>0\) such that
\(|\varphi_\mathtt{i}-\varphi_\mathtt{j}| \ge \eta\mathrm{diam}(\varphi_\mathtt{i}(X))\) for all
\(\mathtt{i},\mathtt{j} \in I^*\) with \(\varphi_\mathtt{i} \ne \varphi_\mathtt{j}\).
By Theorem 4, the WSC can be thought to be a version of the OSC that allows exact overlaps.
Theorem 5 (Zerner (1996) and Fraser-Henderson-Olson-Robinson (2015)).
If \(X \subset \mathbb{R}^2\) is a self-similar set and \(s = \dim_{\mathrm{H}}(X) < 1\), then the following conditions are equivalent:
(1) \(X\) satisfies the WSC,
(2) \(X\) is Ahlfors \(s\)-regular,
(3) \(\mathcal{H}^s(X)>0\),
(4) \(\dim_{\mathrm{L}}(X)=\dim_{\mathrm{H}}(X)=\dim_{\mathrm{A}}(X)\).
The assumption \(\dim_{\mathrm{H}}(X) \le 1\) in the above theorem is essential. Farkas-Fraser (2015) demonstrated that for each \(1 < s \le 2\) there exists an Ahlfors \(s\)-regular self-similar set not satisfying the WSC.
Planar self-affine sets
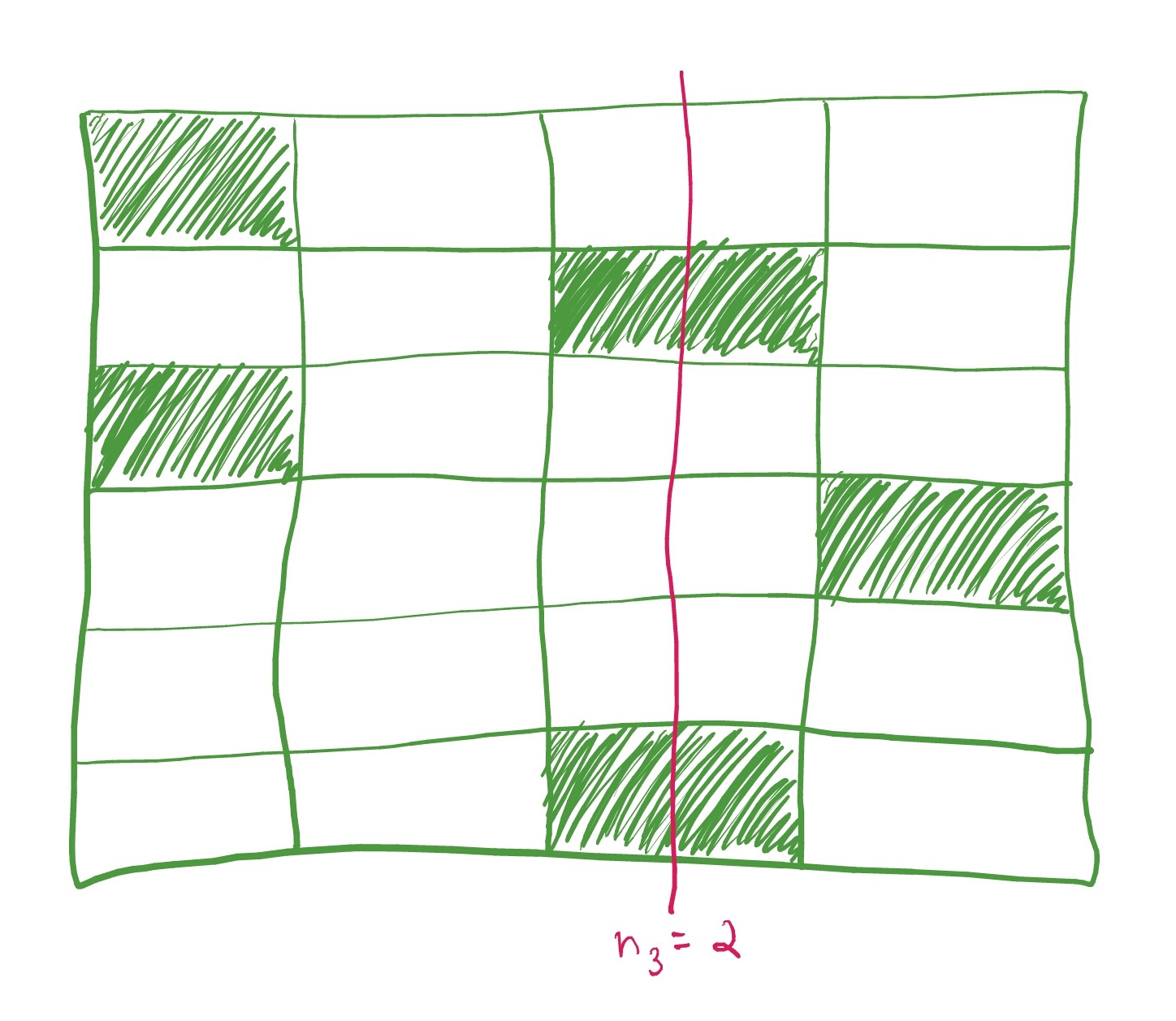
Let \(q > p \ge 2\) and \(\Phi = (A_1+t_1,\ldots,A_N+t_N)\) be an affine IFS such that
\[\begin{equation*}
A_i =
\begin{pmatrix}
\tfrac{1}{p} & 0 \\
0 & \tfrac{1}{q}
\end{pmatrix}
\qquad\text{and}\qquad
t_i = (\tfrac{a_i}{p},\tfrac{b_i}{q}),
\end{equation*}\]
where \(a_i \in \{0,\ldots,p-1\}\) and \(b_i \in \{0,\ldots,q-1\}\).
Write \(n_j = \#\{i \in I : a_i=j\}\). The associated self-affine set \(X \subset \mathbb{R}^2\), the Bedford-McMullen carpet, has uniform vertical fibers if there is \(n \in \mathbb{N}\) such that \(n_j = n\) for all \(j\) with \(n_j \ne 0\).
Theorem 6 (McMullen (1984), Peres (1994), and Mackay (2011)).
If \(X \subset \mathbb{R}^2\) is a Bedford-McMullen carpet and \(s = \dim_{\mathrm{H}}(X),\) then the following conditions are equivalent:
(1) \(X\) has uniform vertical fibers,
(2) \(\mathcal{H}^s(X) < \infty\),
(3) \(X\) is Ahlfors \(s\)-regular,
(4) \(\dim_{\mathrm{L}}(X) = \dim_{\mathrm{H}}(X) = \dim_{\mathrm{A}}(X)\).
Let us consider more general matrices. The singular value function of \(A \in \mathrm{GL}_2(\mathbb{R})\) is
\[\begin{equation*}
\varphi^s(A) =
\begin{cases}
\|A\|^s, &\text{if } 0 \le s < 1, \\
\|A\|^{2-s}|\det(A)|^{s-1}, &\text{if } 1 \le s < 2, \\
|\det(A)|^{s/2}, &\text{if } s \ge 2.
\end{cases}
\end{equation*}\]
The value \(\varphi^s(A)\) represents a measurement of the \(s\)-dimensional volume of the ellipse \(A(B(0,1))\).
If \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_2(\mathbb{R})^N\) and \(s \ge 0\), then the pressure is
\[P(\mathsf{A},s) = \lim_{n \to \infty} \frac{1}{n} \log\sum_{\mathtt{i} \in I^n} \varphi^s(A_\mathtt{i}).\]
The affinity dimension of a self-affine set \(X\), \(\dim_{\mathrm{aff}}(X)\), is the unique \(s \ge 0\) for which \(P(\mathsf{A},s)=0\). If \(X\) is self-similar, then \(\dim_{\mathrm{aff}}(X) = \dim_{\mathrm{sim}}(X)\). Similar to Lemma 2, the affinity dimension is an upper bound for the Hausdorff dimension:
Lemma 7 (Falconer (1988)).
If \(X \subset \mathbb{R}^2\) is a self-affine set, then \(\dim_{\mathrm{H}}(X) \le \min\{2,\dim_{\mathrm{aff}}(X)\}\).
Surprisingly often the affinity dimension is also a lower bound. Let \(\mathbb{RP}^1\) be the real projective line, that is, the set of all lines through the origin in \(\mathbb{R}^2\).
The tuple \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_2(\mathbb{R})^N\) is irreducible if there is no proper linear subspace \(V \in \mathbb{RP}^1\) of \(\mathbb{R}^2\) such that \(A_iV=V\) for all \(i\).
Recall that the set of all irreducible tuples \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is open, dense, and of full Lebesgue measure in \(\mathrm{GL}_2(\mathbb{R})^N\).
The tuple \(\mathsf{A}\) is strongly irreducible if there is no finite collection of proper linear subspaces \(\mathcal{V}\) of \(\mathbb{R}^2\) such that \(A_i\mathcal{V}=\mathcal{V}\) for all \(i\).
Theorem 8 (Feng-K (2011)).
If \(X \subset \mathbb{R}^2\) is an irreducible self-affine set and \(s = \dim_{\mathrm{aff}}(X)\), then \(\mathcal{H}^s(X)<\infty\).
A matrix \(A \in \mathrm{GL}_2(\mathbb{R})\) is proximal if it has two real eigenvalues with different absolute values.
A self-affine set \(X\) satisfies the strong separation condition (SSC) if \(\varphi_i(X) \cap \varphi_j(X) = \emptyset\) for \(i \ne j\). Note that the SSC implies the OSC. The following breakthrough result shows that for “most” planar self-affine sets the affinity dimension is also a lower bound for the Hausdorff dimension:
Theorem 9 (Bárány-Hochman-Rapaport (2019)).
If \(X \subset \mathbb{R}^2\) is a strongly irreducible proximal self-affine set satisfying the SSC, then
\[\begin{align*}
\dim_{\mathrm{H}}(X) &= \min\{2,\dim_{\mathrm{aff}}(X)\}, \\
\dim_{\mathrm{H}}(\mathrm{proj}_{V^\bot}(X)) &= \min\{1,\dim_{\mathrm{aff}}(X)\}
\end{align*}\]
for all \(V \in \mathbb{RP}^1\).
The result gives motivation for further questions. Under the assumptions of the theorem, is it possible to acquire more refined geometric information? When is the Hausdorff measure of the planar self-affine set positive, \(\mathcal{H}^s(X)>0\) for \(s=\dim_{\mathrm{H}}(X)\)? Can the Ahlfors regularity of planar self-affine sets be characterized? What is the Assouad dimension of the set and its projections? Can Marstrand’s slicing theorem be obtained for all slices, i.e. what is the Hausdorff dimension of slices \(X \cap (V+x)\)? Following Bárány-K-Yu (2021+), we manage to present some answers to these questions.
Marstrand’s slicing theorem on planar self-affine sets
A tuple \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_2(\mathbb{R})^N\) is dominated if there exists a closed multicone \(\mathcal{C}\) as a proper subset of \(\mathbb{RP}^1\) such that
\[A_i\mathcal{C} \subset \mathcal{C}^o\]
for every \(i\). For example, if the matrices \(A_i\) have positive entries, then \(\mathsf{A}\) is dominated. A dominated tuple is always proximal.
If \(\mathsf{A}\) is dominated, then \((A_1^{-1},\ldots,A_N^{-1})\) is as well, with multicone \(\overline{\mathbb{RP}^1 \setminus \mathcal{C}}\),
and the set of Furstenberg directions is
\[X_F = \bigcap_{n=1}^\infty \bigcup_{\mathtt{i} \in I^n} A_\mathtt{i}^{-1} \overline{\mathbb{RP}^1 \setminus \mathcal{C}}.\]
Note that \(X_F\) is perfect unless it is a singleton.
Theorem 10 (Bárány-K-Yu (2021+)).
If \(X \subset \mathbb{R}^2\) is a dominated self-affine set satisfying the SSC such that \(\dim_{\mathrm{H}}(X) \ge 1\) and \(X_F\) is not a singleton, then
\[\dim_{\mathrm{A}}(X) = 1 + \sup_{\genfrac{}{}{0pt}{}{x\in X}{V\in X_F}}\dim_{\mathrm{H}}(X\cap(V+x)) < 2.\]
We will sketch the proof, but let us first go through some of the ingredients needed.
Marstrand’s projection theorem states that, given a Borel set \(X \subset \mathbb{R}^2\), we have
\[\dim_{\mathrm{H}}(\mathrm{proj}_{V^\bot}(X)) = \min\{1,\dim_{\mathrm{H}}(X)\}\]
for Lebesgue-almost all \(V \in \mathbb{RP}^1\).
Recall that, for “generic” self-affine sets \(X\), the result of Bárány-Hochman-Rapaport extends the above for all \(V \in \mathbb{RP}^1\).
Marstrand’s projection theorem is a strong dimension conservation principle for Hausdorff dimension:
If \(\dim_{\mathrm{H}}(X) \le 1\), then the dimension of \(X\) is conserved by almost every projection.
If \(\dim_{\mathrm{H}}(X) > 1\), then the same cannot be true, as the projections have dimension at most one in every direction.
This defect is resolved by the classical Marstrand’s slicing theorem. It shows that almost every fiber of a projection do not store more dimension than what is the surplus. The theorem states that, given a Borel set \(X \subset \mathbb{R}^2\) and \(V \in \mathbb{RP}^1\), we have
\[\dim_{\mathrm{H}}(X \cap (V+x)) \le \max\{0,\dim_{\mathrm{H}}(X) - 1\}\]
for Lebesgue almost all \(x \in V^\bot\).
The second main ingredient needed in the proof is the characterization of the Assouad dimension via weak tangent sets. A set \(T\) is a weak tangent of \(X\) if there exist sequences \((x_n)_{n \in \mathbb{N}}\) and \((r_n)_{n \in \mathbb{N}}\) such that \(x_n \in X\) and \(r_n>0\) with \(r_n \to 0\) such that
\[M_{x_n,r_n}(X) \cap B(0,1) \to T\]
in Hausdorff distance, where \(M_{x,r}(z) = \frac{z-x}{r}\). The collection of weak tangents of \(X\) is \(\mathrm{Tan}(X)\). K-Ojala-Rossi (2018) observed that if \(X\) is compact, then
\[\dim_{\mathrm{A}}(X) = \max\{\dim_{\mathrm{H}}(T) : T \in \mathrm{Tan}(X)\}.\]
We are now ready to sketch the proof of Theorem 10:
Proof. To simplify, the idea in the proof is the following: First show that there exists \(T \in \mathrm{Tan}(X)\) such that \(T = L \times W\), \(W\) contains a projected copy of \(X\), and for every \(V \in X_F\) and \(x \in X\) the set \(L\) contains an affine copy of \(X \cap (V+x)\). Since \(\dim_{\mathrm{H}}(W)=1\), Marstrand’s slicing theorem shows that
\[\dim_{\mathrm{A}}(X) \ge \dim_{\mathrm{H}}(T) \ge 1 + \dim_{\mathrm{H}}(X \cap (V+x)).\]
To show the upper bound, relying on K-Ojala-Rossi (2018) choose \(T \in \mathrm{Tan}(X)\) such that \(\dim_{\mathrm{A}}(X)=\dim_{\mathrm{H}}(T)\) and construct a rank one affine map \(G\) so that \(G(T) \subset X\) and \(\textrm{im}(G) \in X_F\). Then
\[\begin{align*}
\sup_{\genfrac{}{}{0pt}{}{x\in X}{V\in X_F}}\dim_{\mathrm{H}}(X\cap(V+x)) &\ge \dim_{\mathrm{H}}(X \cap G(T)) = \dim_{\mathrm{H}}(\mathrm{proj}_{\textrm{ker}(G)^\bot}(T)) \\
&\ge \dim_{\mathrm{H}}(T)-1 = \dim_{\mathrm{A}}(X)-1
\end{align*}\]
as required. ■
Since, by Theorem 9, Marstrand’s projection theorem extends to all \(V \in \mathbb{RP}^1\), it is interesting to ask if also Marstrand’s slicing theorem extends for all fibers \(X \cap (V+x)\).
Furstenberg (1970) conjectured that for the product \(X\) of \(\times 2\) and \(\times 3\) invariant sets all fibers should have Hausdorff dimension at most
\[\max\{0,\dim_{\mathrm{H}}(X) - 1\}.\]
In our terminology, such sets appear as certain dynamically defined subsets of Bedford-McMullen carpets.
Furstenberg’s conjecture was resolved independently by Shmerkin (2019) and Wu (2019).
Example 11 (Bárány-K-Yu (2021+)).
There exists a dominated self-affine set \(X \subset \mathbb{R}^2\) satisfying the SSC such that \(\dim_{\mathrm{H}}(X) \ge 1\) and \(X_F\) is not a singleton such that
\[\dim_{\mathrm{L}}(X) < \dim_{\mathrm{H}}(X) = \dim_{\mathrm{aff}}(X) < \dim_{\mathrm{A}}(X).\]
As an immediate corollary of Theorem 10, we see that such a self-affine set satisfies
\[\dim_{\mathrm{H}}(X)-1 < \dim_{\mathrm{A}}(X)-1 = \sup_{\genfrac{}{}{0pt}{}{x\in X}{V\in X_F}}\dim_{\mathrm{H}}(X\cap(V+x)) < 1.\]
In particular, there exist a fiber \(X \cap (V+x)\) of a projection \(\mathrm{proj}_{V^\bot}\) such that
\[\dim_{\mathrm{H}}(X\cap(V+x)) > \dim_{\mathrm{H}}(X)-1 \ge 0.\]
Thus it is not possible to extend the Marstrand’s slicing theorem on all planar self-affine sets.
Ahlfor regularity of planar self-affine sets
We managed to calculate the lower dimension of a planar self-affine set:
Theorem 12 (Bárány-K-Yu (2021+)).
If \(X \subset \mathbb{R}^2\) is a strongly irreducible proximal self-affine set satisfying the SSC, then
\[\dim_{\mathrm{L}}(X) = \min\{1,\dim_{\mathrm{H}}(X)\}.\]
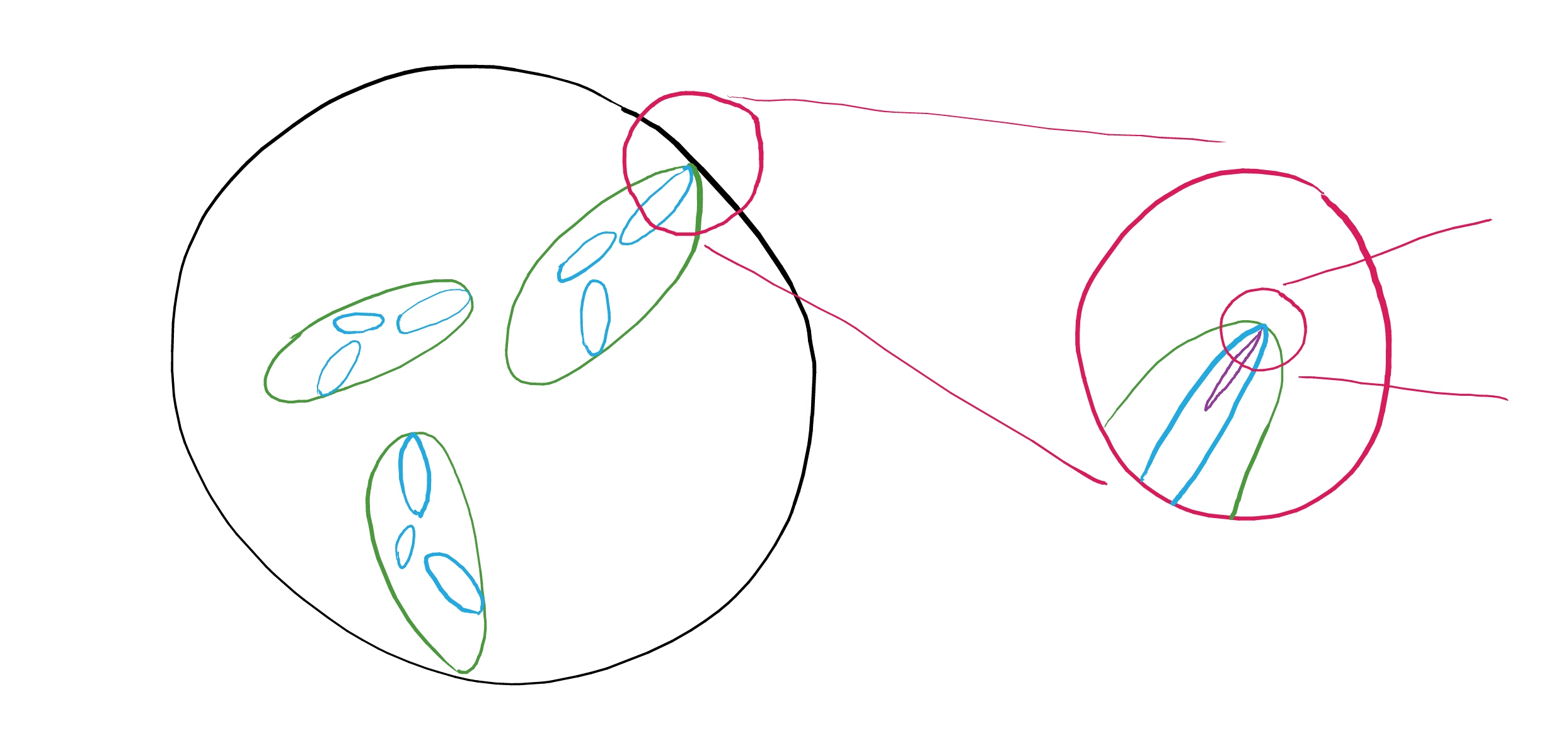
Fraser-Howroyd-K-Yu (2019) observed that if \(X\) is compact, then, analogously to the characterization of the Assouad dimension by tangent sets, we have
\[\dim_{\mathrm{L}}(X) = \min\{\dim_{\mathrm{H}}(T) : T \in \mathrm{Tan}(X)\}.\]
With this result, the adjacent illustration sketches the main idea of the proof.
Note that \((\mathrm{proj}_{V}A)^\top = A^\top \mathrm{proj}_{V}\) and hence, \(\|A^\top|V^\bot\| = \|\mathrm{proj}_{V^\bot}A\|\)
for all \(A \in \mathrm{GL}_2(\mathbb{R})\) and \(V \in \mathbb{RP}^1\).
If \((A_1,\ldots,A_N) \in \mathrm{GL}_2(\mathbb{R})^N\) is dominated, then there is a constant \(C \ge 1\) such that
\[D^{-1}\|A_\mathtt{i}\| \le \|\mathrm{proj}_{V^\bot}A_\mathtt{i}\| \le \|A_\mathtt{i}\|\]
for all \(\mathtt{i} \in I^*\) and \(V \in X_F\).
A self-affine set \(X\) satisfies a projective open set condition (POSC) if there is \(\eta>0\) such that for every \(V \in X_F\) and \(\mathtt{i},\mathtt{j} \in \Sigma_*\) with \(\mathtt{i}\ne\mathtt{j}\) there is \(x \in X\) such that
\[|\mathrm{proj}_{V^\perp}(\varphi_\mathtt{i}(x)-\varphi_\mathtt{j}(x))| \ge \eta\|\mathrm{proj}_{V^\bot}A_\mathtt{i}\|.\]
Theorem 13 (Bárány-K-Yu (2021+)).
If \(X \subset \mathbb{R}^2\) is a dominated self-affine set satisfying the SSC such that \(X_F\) is not a singleton and \(s=\dim_{\mathrm{H}}(X) \le 1\), then the following conditions are equivalent:
(1) \(X\) satisfies the POSC,
(2) \(X\) is Ahlfors \(s\)-regular,
(3) \(\mathcal{H}^s(X)>0\),
(4) \(\inf_{V \in X_F} \mathcal{H}^{s}_\infty(\mathrm{proj}_{V^\perp}(X)) > 0\),
(5) \(\mathrm{proj}_{V^\perp}(X)\) is Ahlfors \(s\)-regular for all \(V \in X_F\).
If \(s=\dim_{\mathrm{H}}(X) < 1\), then we can add the following to the list of equivalent conditions:
(6) \(\dim_{\mathrm{L}}(X)=\dim_{\mathrm{H}}(X)=\dim_{\mathrm{A}}(X)\).
In fact, if any of the conditions (1)–(5) does not hold, then \(\dim_{\mathrm{A}}(X) \ge 1\).
These two results now allow us characterize Ahlfors regularity of planar self-affine sets:
Corollary 14 (Bárány-K-Yu (2021+)).
If \(X \subset \mathbb{R}^2\) is a dominated irreducible self-affine set satisfying the SSC, then the following conditions are equivalent:
(1) \(X\) is Ahlfors \(s\)-regular,
(2) \(0 \le s \le 1\) and \(\mathcal{H}^s(X)>0\).
Proof. If \(s=\dim_{\mathrm{H}}(X)>1\), then, by Theorem 12,
\[\dim_{\mathrm{L}}(X) = \min\{1,\dim_{\mathrm{H}}(X)\} = 1 < \dim_{\mathrm{H}}(X)\]
and \(X\) cannot be Ahlfors \(s\)-regular.
If \(s=\dim_{\mathrm{H}}(X) \le 1\), then, by Theorem 13, \(X\) is Ahlfors \(s\)-regular if and only if \(\mathcal{H}^s(X)>0\). ■
Projections of planar self-affine set
Orponen (2021) proved a strong variant of Marstrand’s projection theorem for Assouad dimension. It states that, given a set \(X \subset \mathbb{R}^2\), we have
\[\dim_{\mathrm{A}}(\mathrm{proj}_{V^\bot}(X)) \ge \min\{1,\dim_{\mathrm{A}}(X)\}\]
for all \(V \in \mathbb{RP}^1 \setminus E\), where the set \(E \subset \mathbb{RP}^1\) satisfies \(\dim_{\mathrm{H}}(E)=0\).
Fraser-K (2020) showed that for every upper semi-continuous function \(f \colon \mathbb{RP}^1 \to [0,1]\) there exists a compact set \(X \subset \mathbb{R}^2\) with \(\dim_{\mathrm{A}}(X)=0\) such that
\[\dim_{\mathrm{A}}(\mathrm{proj}_{V^\bot}(X)) = f(V)\]
for all \(V \in \mathbb{RP}^1\). Therefore, in general, besides proving the exceptional set \(E\) countable, Orponen’s result cannot be improved.
Corollary 15 (Bárány-K-Yu (2021+)).
Let \(X \subset \mathbb{R}^2\) be a dominated irreducible self-affine set satisfying the SSC.
If \(X\) is not Ahlfors regular, then
\[\dim_{\mathrm{A}}(\mathrm{proj}_{V^\bot}(X)) = \min\{1,\dim_{\mathrm{A}}(X)\}\]
for all \(V \in \mathbb{RP}^1 \setminus E\), where the set \(E \subset \mathbb{RP}^1\) satisfies \(\dim_{\mathrm{H}}(E)=0\).
Furthermore, if \(X\) is Ahlfors regular, then the above holds for all \(V \in X_F\).
Proof. If \(X\) is not Ahlfors regular, then Theorem 13 guarantees \(\dim_{\mathrm{A}}(X) \ge 1\). By Orponen (2021), we have
\[1 \ge \dim_{\mathrm{A}}(\mathrm{proj}_{V^\bot}(X)) \ge \min\{1,\dim_{\mathrm{A}}(X)\} = 1\]
for all \(V \in \mathbb{RP}^1\). If \(X\) is Ahlfors \(s\)-regular, then it follows from Corollary 14 and Theorem 13 that \(\dim_{\mathrm{A}}(X) \le 1\) and \(\mathrm{proj}_{V^\bot}(X)\) is Ahlfors \(s\)-regular for all \(V \in X_F\). Therefore,
\[\dim_{\mathrm{A}}(\mathrm{proj}_{V^\bot}(X)) = \dim_{\mathrm{A}}(X) = \min\{1,\dim_{\mathrm{A}}(X)\}\]
as claimed. ■