Rigidity of quasisymmetric maps on self-affine carpets
Quasisymmetric maps
We consider the behavior of quasisymmetric maps on self-affine carpets. More precisely, we study what kind of restrictions does the structure of self-affine carpets \(E\) and \(F\) give to quasisymmetric maps \(f \colon E \to F\). We also show that such self-affine carpets are minimal for the conformal dimension.
If \((X,d)\) and \((Y,\varrho)\) are metric spaces and \(\eta \colon [0,\infty) \to [0,\infty)\) is a homeomorphism, then a homeomorphism \(f \colon X \to Y\) is \(\eta\)-quasisymmetric if
\[\frac{\varrho(f(x),f(y))}{\varrho(f(x),f(z))} \le \eta\biggl( \frac{d(x,y)}{d(x,z)} \biggr)\]
for all \(x,y,z \in X\) with \(x \ne z\). Quasisymmetric maps generalize bi-Lipschitz maps, but compared to arbitrary homeomorphisms, their local behavior has some control:
Lemma 1.
If \(f \colon X \to Y\) is an \(\eta\)-quasisymmetric map, then for each \(x \in X\) and \(r > 0\) there is \(t > 0\) such that
\[B(f(x),t) \subset f(B(x,r)) \subset B(f(x),2\eta(1)t).\]
Proof. Choose \(z,y \in Y\) as in the following picture:
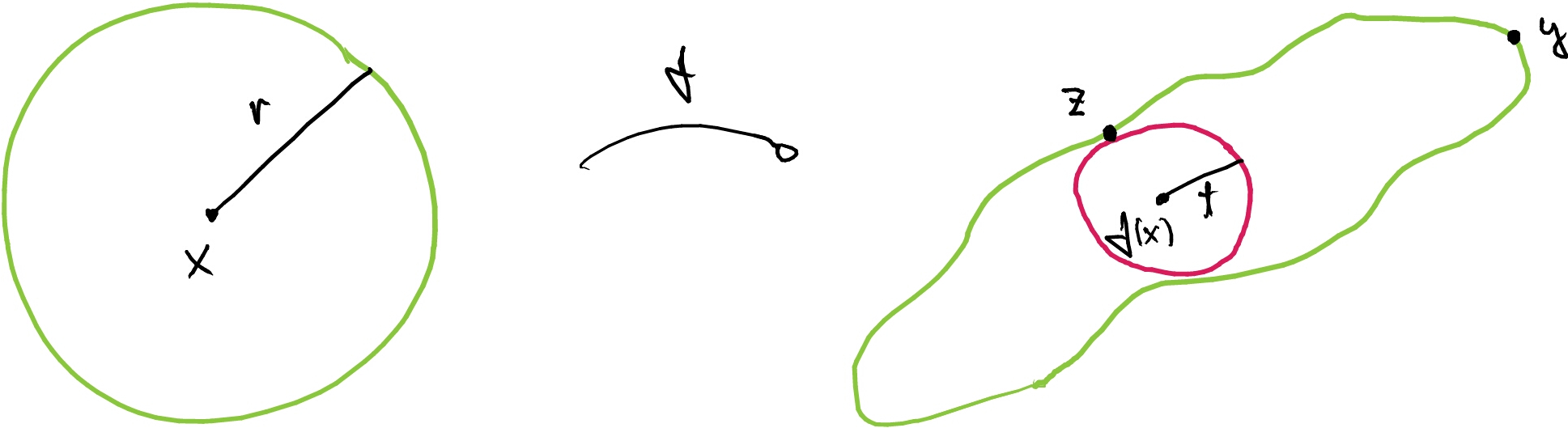
Let \(t = \varrho(f(x),z)\). Then we clearly have
\[B(f(x),t) \subset f(B(x,r)) \subset B(f(x),2\varrho(f(x),y)).\]
Since
\[\varrho(f(x),y) = \frac{\varrho(f(x),y)}{\varrho(f(x),z)} t \le \eta\biggl( \frac{d(x,f^{-1}(y))}{d(x,f^{-1}(z))} \biggr) t \le \eta(1) t,\]
this gives the claim. ■
A metric space is uniformly perfect if there exists a constant \(D \ge 1\) such that \(B(x,r) \setminus B(x,r/D) \ne \emptyset\) for all \(x \in X\) and \(r > 0\) whenever \(X \setminus B(x,r) \ne \emptyset\). The following lemma further describes properties of quasisymmetric maps:
Lemma 2.
If \(X\) and \(Y\) are uniformly perfect bounded metric spaces and \(f \colon X \to Y\) is a quasisymmetric map, then there are \(\Lambda \ge \lambda > 0\) such that
\[cd(x,y)^\Lambda \le \varrho(f(x),f(y)) \le Cd(x,y)^\lambda\]
for all \(x,y \in X\).
The Assouad dimension of a set \(E\), denoted by \(\dim_{\mathrm{A}}(E)\), is the infimum of all \(s\) satisfying the following: there exists a constant \(C \ge 1\) such that each set \(E \cap B(x,R)\) can be covered by at most \(C(R/r)^t\) balls of radius \(r\) centered at \(E\) for all \(0 < r < R\). The definition is due to Assouad (1983). Recall that the Hausdorff dimension of \(E\), \(\dim_{\mathrm{H}}(E)\), is defined by using arbitrary covers and the upper Minkowski dimension of \(E\), \(\overline{\dim}_{\mathrm{M}}(E)\), uses covers consisting of balls having the same radius. The upper Minkowski dimension is therefore related to the average small scale structure whereas the Assouad dimension depends on the extreme properties of the set and takes into account all scales. In fact, if \(E \subset X\) is compact, then \(\dim_{\mathrm{H}}(E) \le \overline{\dim}_{\mathrm{M}}(E) \le \dim_{\mathrm{A}}(E)\). Furthermore, Assouad dimension is invariant under bi-Lipschitz maps but, contrary to the Hausdorff dimension and the upper Minkowski dimension, it may increase under Lipschitz maps.
A metric space \(X\) is doubling if there exists \(N \in \mathbb{N}\) such that each ball \(B(x,2r)\) can be covered by at most \(N\) many balls of radius \(r\). If \(X\) is a metric space, then \(\dim_{\mathrm{A}}(X) < \infty\) if and only if \(X\) is doubling.
By Naor-Neiman (2012), the Assouad embedding theorem states that for every \(N \in \mathbb{N}\) and \(\tfrac{1}{2} < \varepsilon < 1\) there are \(D=D(N) \in \mathbb{N}\) and \(L = L(N,\varepsilon) > 1\) such that if \((X,d)\) is an \(N\)-doubling metric space, then \((X,d^\varepsilon)\) admits a \(L\)-bi-Lipschitz embedding into \(\mathbb{R}^D\).
A set \(E \subset \mathbb{R}^d\) is porous if there exists \(\tfrac12 < \alpha < 1\) such that for each \(x \in X\) and \(r > 0\) there is \(y\) such that \(B(y,\alpha r) \subset B(x,r) \setminus E\). If \(E \subset \mathbb{R}^d\), then \(\dim_{\mathrm{A}}(E) < d\) if and only if \(E\) is porous.
The conformal Assouad dimension of \(E\) is
\[\mathcal{C}\dim_{\mathrm{A}}(E) = \inf\{ \dim_{\mathrm{A}}(E') : E' \text{ is a quasisymmetric image of } E \}.\]
The Assouad dimension above can of course be replaced by any set dimension, and this gives rise to other conformal dimensions. The definition is due to Pansu (1989). The conformal dimension measures the dimension of the “best shape” of the metric space. We say that a set \(E\) is minimal for the conformal Assouad dimension if
\[\mathcal{C}\dim_{\mathrm{A}}(E) \ge \dim_{\mathrm{A}}(E).\]
Note that we trivially have \(\mathcal{C}\dim_{\mathrm{A}}(E) \le \dim_{\mathrm{A}}(E)\).
If \(E \subset \mathbb{R}\) is porous, then \(\mathcal{C}\dim_{\mathrm{H}}(E)=0\). A nontrivial generalization of this is the result of Kovalev (2006) which states that a metric space \(X\) with \(\dim_{\mathrm{H}}(X) < 1\) has \(\mathcal{C}\dim_{\mathrm{H}}(X)=0\). On the other hand, Tyson (2000) has shown that for each \(1 \le s \le d\) there is \(E \subset \mathbb{R}^d\) such that \(\mathcal{C}\dim_{\mathrm{H}}(E) = \dim_{\mathrm{H}}(E) = s\), so \(E\) is minimal for the conformal Hausdorff dimension.
Recall that bi-Lipschitz maps preserve the dimension. By Marczewski (1937), the topological dimension \(\dim_{\mathrm{T}}(E)\) of a separable set \(E\) is
\[\dim_{\mathrm{T}}(E) = \inf\{ \dim_{\mathrm{H}}(E') : E' \text{ is a homeomorphic image } E \}.\]
Therefore,
\[\dim_{\mathrm{T}}(E) \le \mathcal{C}\dim_{\mathrm{H}}(E) \le \dim_{\mathrm{H}}(E).\]
This observation gives an intuition that a quasisymmetric map defined on a minimal set behaves as an average like a bi-Lipschitz map, and defined on other kinds of sets, starts to resemble a general homeomorphism. Also, since \(\dim_{\mathrm{T}}(\mathbb{R}^d) = d\), it holds that \(\mathcal{C}\dim_{\mathrm{H}}(\mathbb{R}^d) = \mathcal{C}\dim_{\mathrm{A}}(\mathbb{R}^d) = d\).
Horizontal carpets
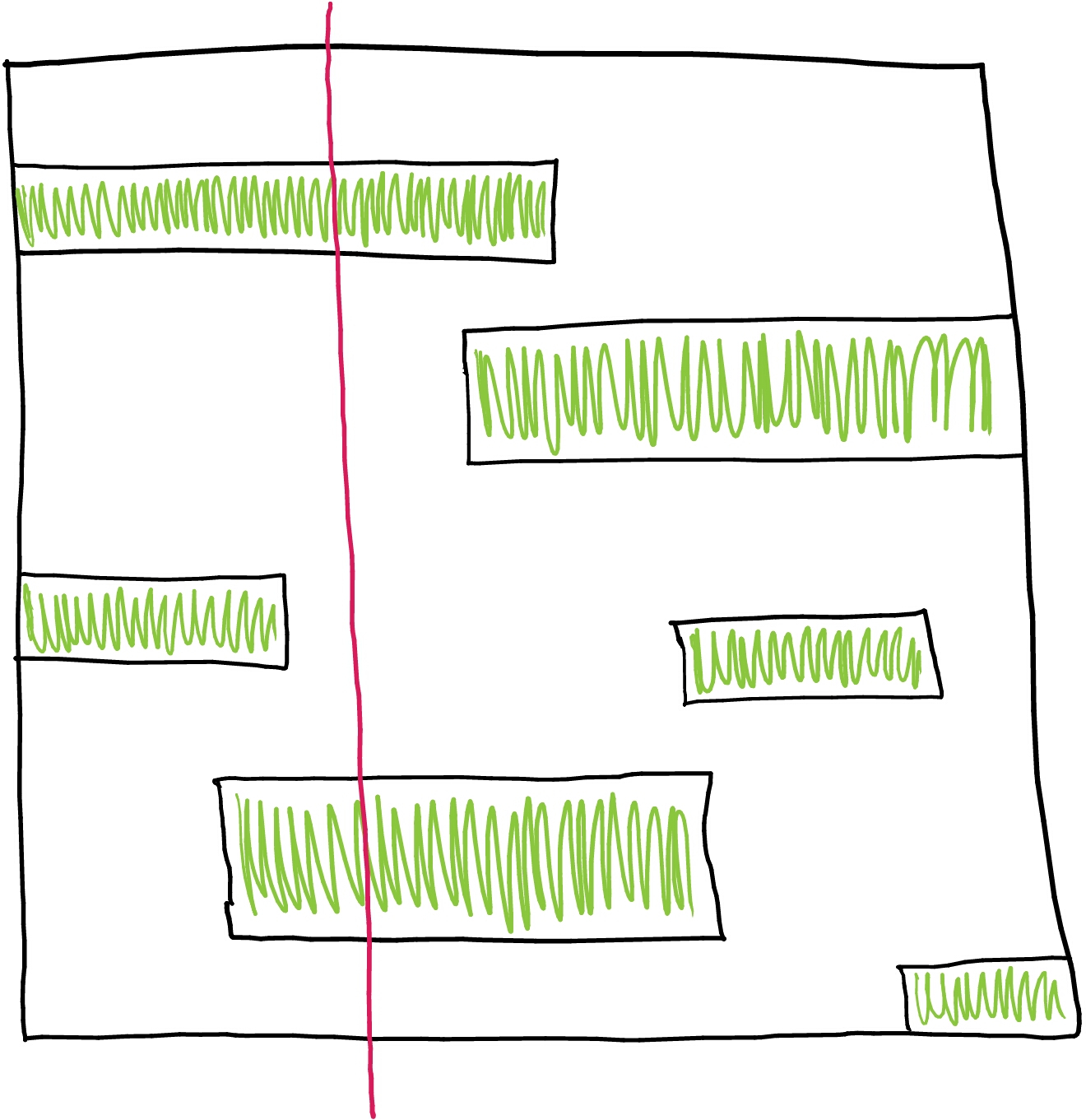
A set \(E \subset \mathbb{R}^2\) is a horizontal self-affine carpet if it satisfies the strong separation condition, the “construction rectangles” are horizontal, and each vertical line intersects at least two such rectangles:
Furthermore, we say that a map \(f \colon X \to Y\) is quasi-Lipschitz if
\[\frac{\log \varrho(f(x),f(y))}{\log d(x,y)} \to 1\]
uniformly as \(d(x,y) \to 0\).
Theorem 3 (K-Ojala-Rossi (2018)).
If \(E,F \subset \mathbb{R}^2\) are horizontal self-affine carpets, then any quasisymmetric map \(E \to F\) is quasi-Lipschitz.
If \(X\) and \(Y\) are separable, then quasi-Lipschitz maps between them preserve the Hausdorff dimension. Therefore, by Theorem 3, two horizontal self-affine carpets either have the same dimension or there are no quasi-symmetric maps between them. This is in a huge contrast to the self-similar case: Wang-Wen-Zhu (2010) have shown that if \(E\) and \(F\) are self-similar sets satisfying the strong separation condition, then there exists a quasisymmetric map \(E \to F\). This means that, in fact, \(\mathcal{C}\dim_{\mathrm{H}}(E)=0\) for all such self-similar sets \(E\). Moreover, Bonk-Merenkov (2013) have shown that every quasisymmetric self-map of the standard Sierpiński carpet is an isometry.
Theorem 4 (K-Ojala-Rossi (2018)).
Horizontal self-affine carpets are minimal for the conformal Assouad dimension.
Mackay (2011) has shown that Gatzouras-Lalley carpets are minimal for the conformal Assouad dimension when they project to a line; otherwise the conformal Assouad dimension is zero. Theorem 4 strictly generalizes the result of Mackay. It should also be mentioned that since the codomains in the definition of the conformal dimension can be any metric spaces, Theorem 3 cannot be used to prove Theorem 4.
About the proofs
The proof of Theorem 3 has the following three essential steps:
Theorem 5.
Let \(X\) and \(Y\) be uniformly perfect compact doubling metric spaces. If \(f \colon X \to Y\) is a quasisymmetric map such that any quasisymmetric weak tangent map is bi-Lipschitz (with the same constants), then \(f\) is quasi-Lipschitz.
Let \(E \subset [0,1]^d\) be compact. We say that \(W\) is a weak tangent of \(E\) if there exists a sequence of similarity maps \(S_n \colon \mathbb{R}^d \to \mathbb{R}^d\) such that
\[S_n(E) \to W\]
in the Hausdorff metric as \(n \to \infty\). The above definition is given in \(\mathbb{R}^d\) only for simplicity. The general case can be handled by the pointed Gromov-Hausdorff convergence and the Assouad embedding. Let \(f \colon E \to E'\) be a quasisymmetric map. If \(W'\) is a tangent set of \(E'\) (and \(S_n'\) the associated similarities), then, by the Arzelà-Ascoli theorem, \(S_n' \circ f \circ S_n^{-1}\) converge (along a subsequence) to a quasisymmetric weak tangent map \(\hat f \colon W \to W'\).
Proof of Theorem 5. The idea of the proof is as follows: If \(f\) is not quasi-Lipschitz, then there exists a sequence of pairs of points in which \(f\) obeys true Hölder behavior. For each pair there is a triplet of points (with comparable distances) in which \(f\) still obeys true Hölder behavior. These triplets then allow us to define weak tangents so that the limit maps are quasisymmetric and obey true Hölder behavior. This is a contradiction with the bi-Lipschitz assumption.
If \(f\) is not quasi-Lipschitz, then there are \(\kappa>0\) and sequences \((x_i)\) and \((y_i)\) such that
\[\varrho(f(x_i),f(y_i)) < d(x_i,y_i)^{1+\kappa}\]
for all \(i\) and \(d(x_i,y_i) \to 0\) as \(i \to \infty\). Relying on uniform perfectness, choose \(z_i^j\) such that \(z_i^0 = y_i\) and
\[d(x_i,y_i) \approx \varepsilon d(x_i,z_i^1) \approx \varepsilon^2d(x_i,z_i^2) \approx \cdots\]
We assume that
\[\varrho(f(x_i),f(z_i^{j-1})) \ge \varepsilon^{1+\kappa/2} \varrho(f(x_i),f(z_i^j))\]
for all \(j\). This would mean that the distances \(\varrho(f(x_i),f(z_i^j))\) are above the graph of \(w \mapsto w^{1+\kappa/2}\):
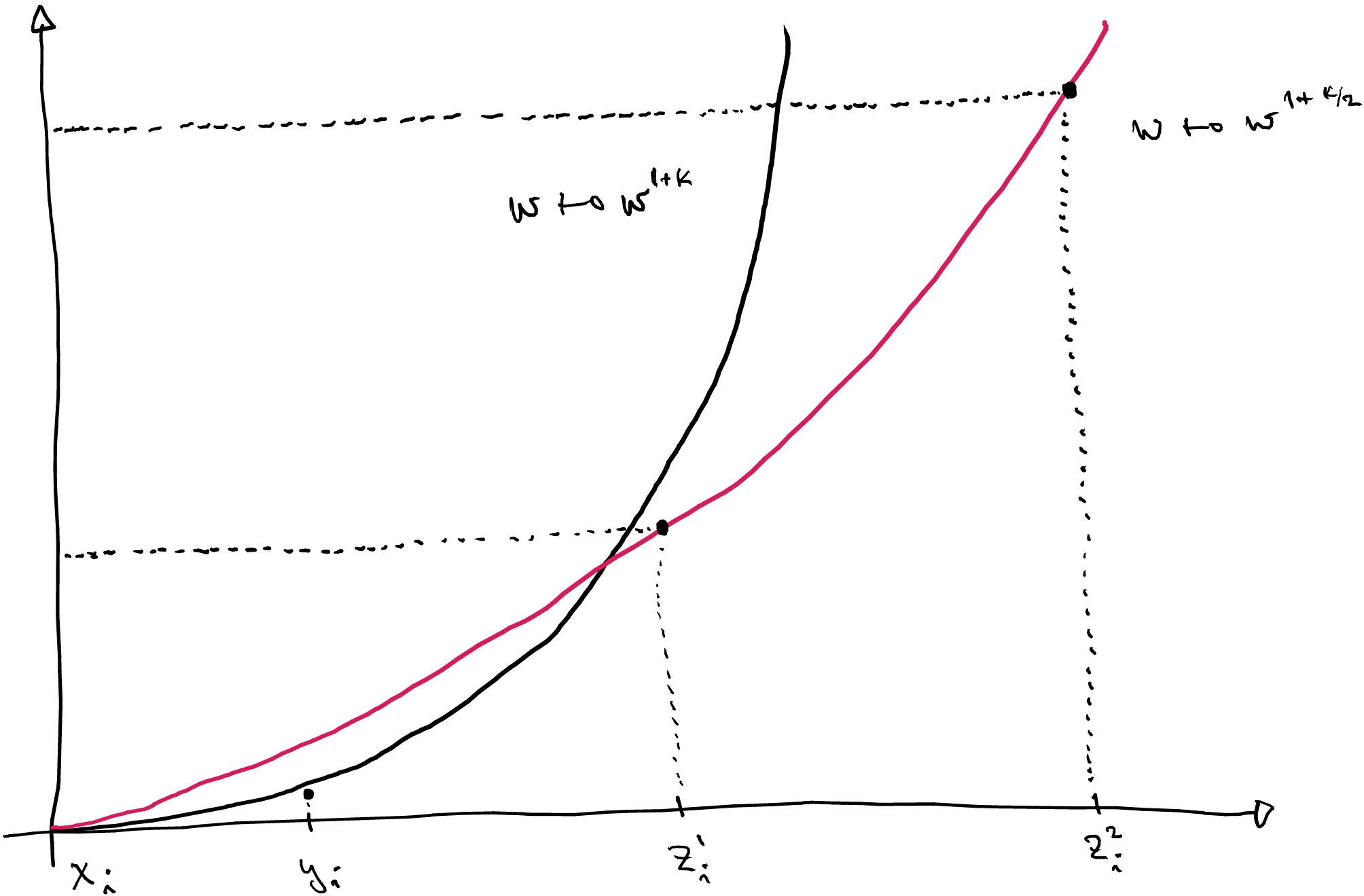
By Hölder continuity and the estimate for \(f(y_i)\), this is a contradiction. Hence there exists \(j\) such that
\[\varrho(f(x_i),f(z_i^{j-1})) < \varepsilon^{1+\kappa/2} \varrho(f(x_i),f(z_i^j)).\]
Let us denote \((x_i,z_i^{j-1},z_i^j)\) by \((a_i,b_i,c_i)\). Define weak tangent sets and map \(\hat f\) by using magnifications which take \(d(a_i,c_i)\) and \(\varrho(f(a_i),f(c_i))\) into unit lengths. Let \(a,b,c\) be such that \(a_i\to a\), \(b_i\to b\), and \(c_i\to c\). Recalling that \(\hat f\) is bi-Lipschitz, we get
\[\varepsilon = \varepsilon d(a,c) \approx d(a,b) \approx \varrho(\hat f(a),\hat f(b)) \approx \frac{\varrho(f(a_i),f(b_i))}{\varrho(f(a_i),f(c_i))} < \varepsilon^{1+\kappa/2},\]
which is a contradiction for small enough \(\varepsilon > 0\). ■
The task is now to find geometric conditions under which the assumptions of Theorem 5 are satisfied. These are given by the following result. A metric space \(X\) is fibered if \(X = \bigcup_i F_i\), where the fibers \(F_i\) are unbounded geodesic spaces and they have positive distance. Furthermore, non-parallel fibers are assumed to diverge and parallel fibers are not isolated.
Theorem 6 (Le Donne-Xie (2016)).
If \(X\) and \(Y\) are fibered spaces and \(f \colon X \to Y\) is a quasisymmetric map such that the fibers of \(X\) go homeomorphically to fibers of \(Y\), then \(f\) is bi-Lipschitz.
Theorem 3 follows from Theorem 5 and Theorem 6 if weak tangents of horizontal self-affine carpets are unions of fibered spaces. This is the content of the last step of the proof:
Theorem 7.
If \(E\) is a horizontal self-affine carpet, then the weak tangents of \(E\) are of the form
\[(-\infty,\omega] \times C_{\mathrm{left}} \cup [\omega,\infty) \times C_{\mathrm{right}},\]
where \(C_{\mathrm{left}}\) and \(C_{\mathrm{right}}\) are uniformly perfect porous sets.
Theorem 7 generalizes the result of Bandt-K (2013) which describes tangent sets at generic points under some assumptions. The result of Bandt-K has recently been generalized for non-carpet self-affine sets by K-Koivusalo-Rossi (2017).
The proof of Theorem 4 relies on the following two results. The first one guarantees that the weak tangents of a horizontal self-affine carpet are minimal.
Theorem 8 (Bishop-Tyson (2001)).
If \(C \subset \mathbb{R}^{d-1}\) is compact, then \([0,1] \times C \subset \mathbb{R}^d\) is minimal for the conformal Hausdorff dimension.
The second one states that the Assouad dimension is characterized by weak tangents. This important observation is goes back to the work of Furstenberg (2008). The connection to the Assouad dimension was noticed in K-Rossi (2016) and below:
Theorem 9.
If \(E \subset \mathbb{R}^d\) is compact, then there exists a weak tangent \(W\) of \(E\) such that
\[\dim_{\mathrm{H}}(W) = \dim_{\mathrm{A}}(E).\]
Let \(E \subset \mathbb{R}^2\) be a horizontal self-affine carpet. By Theorem 9, there exists a weak tangent \(W\) of \(E\) such that
\(\dim_{\mathrm{A}}(E) = \dim_{\mathrm{H}}(W)\). Recall that, by Theorem 7, \(W\) is a union of fibered spaces. Therefore, by Theorem 8, \(W\) is minimal for the conformal Hausdorff dimension, i.e.
\(\dim_{\mathrm{H}}(W) \le \mathcal{C}\dim_{\mathrm{H}}(W) \le \mathcal{C}\dim_{\mathrm{A}}(W)\).
Recalling the definition of the Assouad dimension, it is easy to see that \(\dim_{\mathrm{A}}(W) \le \dim_{\mathrm{A}}(E)\) and, similarly,
\(\mathcal{C}\dim_{\mathrm{A}}(W) \le \mathcal{C}\dim_{\mathrm{A}}(E)\).
Theorem 4 follows now by combining these inequalities.