Self-conformal sets with positive Hausdorff measure
A tuple \((\varphi_1,\ldots,\varphi_N)\) of contractive conformal maps \(\varphi_i \colon \mathbb{R}^d \to \mathbb{R}^d\) is called a conformal IFS.
In the real line, we use \(C^{1+\alpha}\)-maps.
There exists unique nonempty compact set \(X \subset \mathbb{R}^d\), the self-conformal set, for which
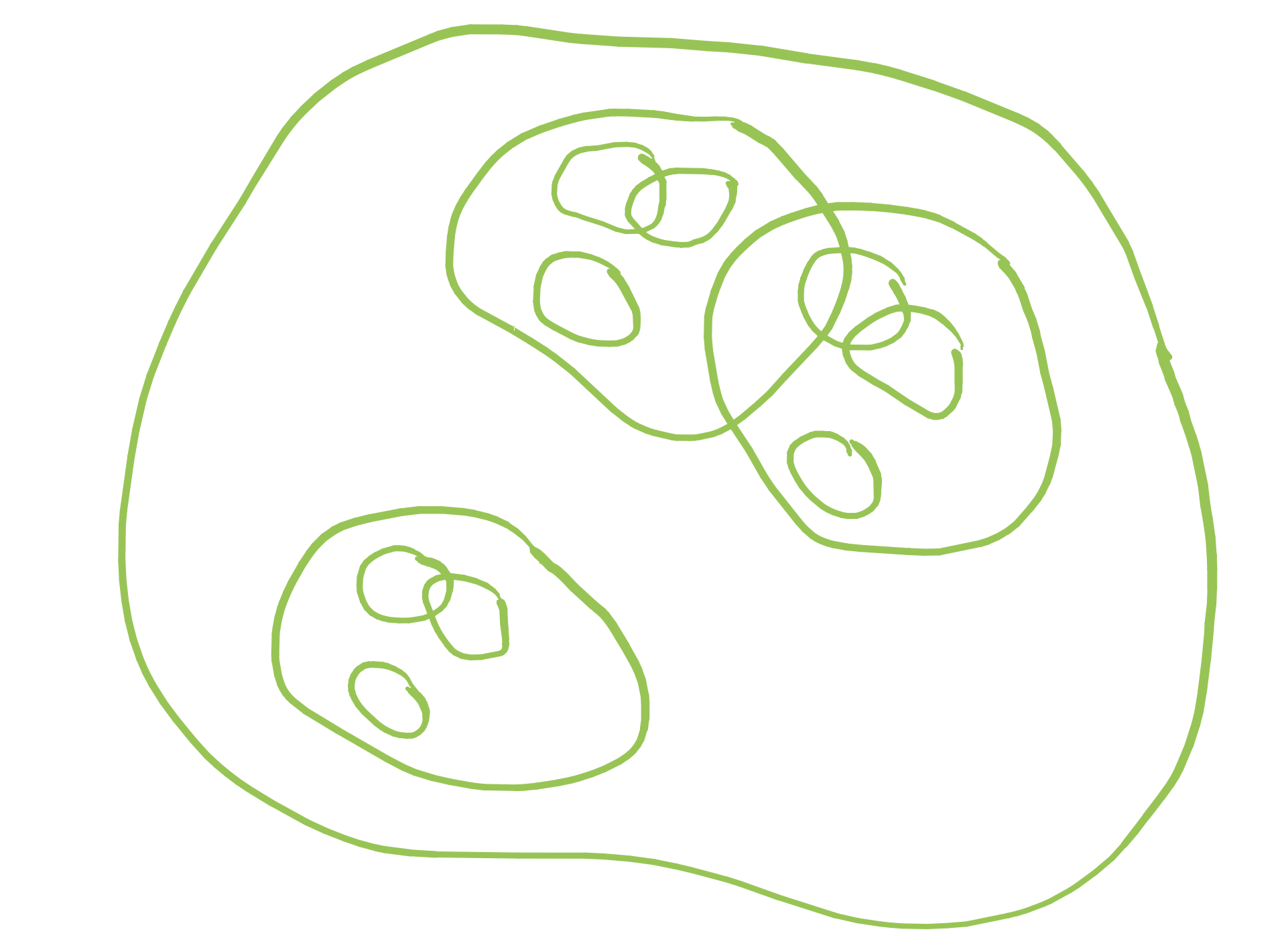
\[X = \bigcup_{i=1}^N \varphi_i(X) = \bigcap_{n \in \mathbb{N}} \bigcup_{\mathtt{i} \in \{1,\ldots,N\}^n} \varphi_\mathtt{i}(B),\]
where \(B\) is a large closed ball and \(\varphi_\mathtt{i} = \varphi_{i_1} \circ \cdots \circ \varphi_{i_n}\) for all \(\mathtt{i} = i_1 \cdots i_n\).
What is the size of \(X\)? If the construction pieces are separated, then \(\dim(X) \approx s\), where
\[\sum_{i=1}^N \mathrm{diam}(\varphi_i(X))^s \approx \sum_{i=1}^N \|\varphi_i'\|^s = 1.\]
Hausdorff content
Recall that the \(s\)-dimensional Hausdorff measure of a set \(A \subset \mathbb{R}^d\) is
\[\mathcal{H}^s(A) = \lim_{\delta \downarrow 0} \mathcal{H}^s_\delta(A) = \sup_{\delta>0} \mathcal{H}^s_\delta(A),\]
where
\[\mathcal{H}^s_\delta(A) = \inf\Bigl\{\sum_i \mathrm{diam}(U_i)^s : A \subset \bigcup_i U_i \text{ and } \mathrm{diam}(U_i) \le \delta\Bigr\}\]
is the Hausdorff \(\delta\)-content of \(A\).
It is well known that \(\mathcal{H}^s\) is a Borel regular measure and \(\mathcal{H}^s_\delta\) is an outer measure—usually highly non-additive and non-Borel.
It is easy to see that \(\mathcal{H}^s(A)=0\) if and only if \(\mathcal{H}^s_\infty(A)=0\).
The Hausdorff dimension of \(A\) is \(\dim_{\mathrm{H}}(A) = \inf\{s:\mathcal{H}^s(A)=0\}\).
Theorem 1 (Angelevska-K-Troscheit (2018+)).
If \(X \subset \mathbb{R}^d\) is a self-conformal set and \(s=\dim_{\mathrm{H}}(X)\), then
\[\mathcal{H}^s(X \cap A) \lesssim \mathcal{H}^s_\infty(X \cap A)\]
for all \(\mathcal{H}^s\)-measurable \(A \subset \mathbb{R}^d\).
This generalizes the result of Farkas-Fraser (2015) in the self-similar case.
It is remarkable to note that their proof does not generalize into the self-conformal case.
Let us next sketch the proof of Theorem 1:
Proof. Assume to the contrary that there exists \(\mathcal{H}^s\)-measurable \(A \subset \mathbb{R}^d\) such that
\(\mathcal{H}^s(X \cap A) \gtrsim \mathcal{H}^s_\infty(X \cap A)\).
Fix \(n \in \mathbb{N}\) and let \(\mathcal{B}\) be a maximal \(2^{-n}\)-packing of balls in \(X\).
It is easy to see that \(\#\mathcal{B} \approx 2^{ns}\).
For each \(B \in \mathcal{B}\) define \(g_B \colon X \to X \cap B\) such that \(|g_B(x)-g_B(y)| \approx 2^{-n}|x-y|\).
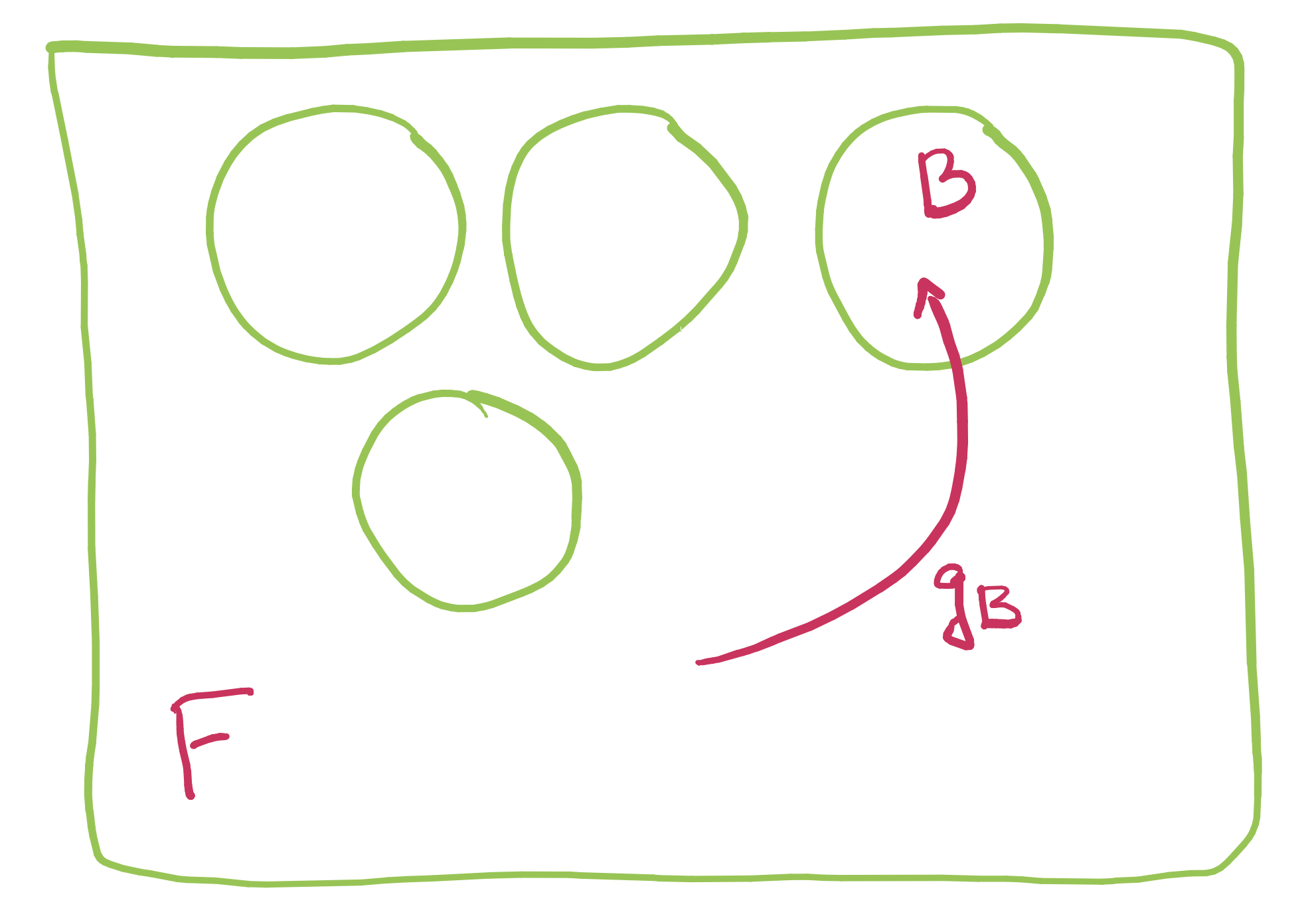
We may assume that the set \(X \cap A\) has measure \(\mathcal{H}^s(X \cap A)>0\) and hence,
\(\mathcal{H}^s(g_B(X \cap A)) \gtrsim 2^{-ns}\mathcal{H}^s(X \cap A)\).
Noting that the set \(X \cap A\) has content \(\mathcal{H}^s_\infty(X \cap A)>0\), we have
\(\mathcal{H}^s_{2^{-n}}(g_B(X \cap A)) \lesssim 2^{-ns}\mathcal{H}^s_\infty(X \cap A)\).
Since
\[\begin{align*}
\mathcal{H}^s(X) &= \sum_{B \in \mathcal{B}} \mathcal{H}^s(g_B(X \cap A)) + \mathcal{H}^s(\textrm{``the rest''}) \\
&\gtrsim \#\mathcal{B} \cdot 2^{-ns} \mathcal{H}^s_\infty(X \cap A) + \mathcal{H}^s(\textrm{``the rest''})
\end{align*}\]
and
\[\begin{align*}
\mathcal{H}^s_{2^{-n}}(X) &\le \sum_{B \in \mathcal{B}} \mathcal{H}^s_{2^{-n}}(g_B(X \cap A)) + \mathcal{H}^s_{2^{-n}}(\textrm{``the rest''}) \\
&\lesssim \#\mathcal{B} \cdot 2^{-ns} \mathcal{H}^s_\infty(X \cap A) + \mathcal{H}^s(\textrm{``the rest''}),
\end{align*}\]
we have
\[\mathcal{H}^s(X) - \mathcal{H}^s_{2^{-n}}(X) \gtrsim \mathcal{H}^s_\infty(X \cap A) > 0\]
for all \(n \in \mathbb{N}\), which is a contradiction. ■
Separation conditions
The pressure \(P \colon [0,\infty) \to \mathbb{R}\) is defined by
\[P(s) = \lim_{n \to \infty} \frac{1}{n}\log\sum_{\mathtt{i} \in \{1,\ldots,N\}^n} \|\varphi_\mathtt{i}'\|^s.\]
It is easy to see that \(\dim_{\mathrm{H}}(X) \le P^{-1}(0)\).
The open set condition (OSC) is satisfied if there exists an open set \(U \subset \mathbb{R}^d\) such that
\(\varphi_i(U) \subset U\) and \(\varphi_i(U) \cap \varphi_j(U) = \emptyset\).
Theorem 2 (Peres-Rams-Simon-Solomyak (2001)).
If \(X \subset \mathbb{R}^d\) is a self-conformal set and \(s=P^{-1}(0)\), then OSC \(\Leftrightarrow\) \(\mathcal{H}^s(X)>0\).
What can be said if \(s = \dim_{\mathrm{H}}(X) < P^{-1}(0)\)?
Roughly speaking, the weak separation condition (WSC) means that it can happen \(\varphi_\mathtt{i} = \varphi_\mathtt{j}\) for some \(\mathtt{i} \ne \mathtt{j}\) but otherwise the OSC is satisfied.
It is easy to see that if there is exact overlapping, i.e. \(\varphi_\mathtt{i} = \varphi_\mathtt{j}\) for some \(\mathtt{i} \ne \mathtt{j}\), then the dimension drops, \(\dim_{\mathrm{H}}(X) < P^{-1}(0)\). The dimension drop conjecture claims that the exact overlapping is the only way to drop the dimension. Hochman (2014) verified the conjecture for all self-similar sets on \(\mathbb{R}\) defined by algebraic parameters.
The proof of Hochman’s result does not generalize to self-conformal sets.
Theorem 3 (Lau-Ngai-Wang (2009)).
If \(X \subset \mathbb{R}^d\) is a self-conformal set and \(s=\dim_{\mathrm{H}}(X)\), then WSC \(\Rightarrow\) \(\mathcal{H}^s(X)>0\).
In the self-similar case, Zerner (1996) introduced the identity limit criterion (ILC), by requiring that
\(\{\varphi_\mathtt{i}^{-1}\circ\varphi_\mathtt{j}\}_{\mathtt{i},\mathtt{j}}\) does not accumulate to the identity,
and showed that it is equivalent to the WSC.
The self-conformal case is more complicated since we cannot use inverses (contractive entire functions are similarities).
Nevertheless, we introduced the ILC in the conformal setting as
\[\inf\{ \|\varphi_\mathtt{i}'\|^{-1} \sup_{x \in X}|\varphi_\mathtt{i}(x)-\varphi_\mathtt{j}(x)| : \varphi_\mathtt{i}|_X \ne \varphi_\mathtt{j}|_X \} > 0\]
and proved that it is equivalent to the WSC.
To be able to do so, we actually had to slightly weaken the original definition of the WSC by restricting the mappings to \(X\).
The Assouad dimension of \(A \subset \mathbb{R}^d\) is
\[\dim_{\mathrm{A}}(A) = \inf\Bigl\{ s \ge 0 : \sup_{x \in A} N_r(A \cap B(x,R)) \lesssim \Bigl( \frac{R}{r} \Bigr)^s \text{ for all } 0<r<R \Bigr\},\]
where \(N_r(A)\) is the least number of balls of radius \(r>0\) required to cover a bounded set \(A\).
It is easy to see that \(\dim_{\mathrm{H}}(A) \le \dim_{\mathrm{A}}(A)\).
Theorem 4 (Angelevska-K-Troscheit (2018+)).
If \(X \subset \mathbb{R}\) is a self-conformal set and \(\dim_{\mathrm{A}}(X)<1\), then \(X\) satisfies the ILC (and hence also the WSC).
The corresponding result in the self-similar case was proved by Fraser-Henderson-Olson-Robinson (2015).
To prove Theorem 4 (and the equivalence ILC \(\Leftrightarrow\) WSC), the main technical observation is the following:
If ILC is not satisfied, then for every \(\varepsilon>0\) there is \(0<\delta<\varepsilon\) and \(\mathtt{i},\mathtt{j}\) such that
\[|\varphi_\mathtt{i}(x)-\varphi_\mathtt{j}(x)| \approx \delta\|\varphi_\mathtt{i}'\| \approx \delta\|\varphi_\mathtt{j}'\|\]
for all \(x\).
The result guarantees the existence of maps which are arbitrary close to each other in the relative scale.
Consequences
A set is Ahlfors \(s\)-regular if it supports a measure \(\mu\) for which \(\mu(B(x,r)) \approx r^s\).
Corollary 5.
If \(X \subset \mathbb{R}^d\) is a self-conformal set and \(s=\dim_{\mathrm{H}}(X)\), then \(\mathcal{H}^s(X)>0\) \(\Leftrightarrow\) \(X\) is Ahlfors \(s\)-regular.
Proof. Suppose that \(X\) is Ahlfors \(s\)-regular. If \(\{U_i\}_i\) is a \(\delta\)-cover of \(X\), then
\(\mu(X) \le \sum_i \mu(U_i) \lesssim \sum_i \mathrm{diam}(U_i)^s\).
Therefore, \(\mathcal{H}^s_\delta(X)\ge\mu(X)>0\) for all \(\delta>0\) and \(\mathcal{H}^s(X)>0\).
Let us then assume that \(\mathcal{H}^s(X)>0\). By Theorem 1,
\[\mathcal{H}^s|_X(B(x,r)) \lesssim \mathcal{H}^s_\infty(X \cap B(x,r)) \lesssim r^s.\]
On the other hand, choose largest subset \(\varphi_\mathtt{i}(X) \subset B(x,r)\). Then
\(|\varphi_\mathtt{i}(x)-\varphi_\mathtt{i}(y)| \approx r|x-y|\) and
\[\mathcal{H}^s|_X(B(x,r)) \ge \mathcal{H}^s(\varphi_\mathtt{i}(X)) \gtrsim \mathcal{H}^s(X)r^s\]
as claimed. ■
Corollary 6.
If \(X \subset \mathbb{R}\) is a self-conformal set and \(s=\dim_{\mathrm{H}}(X)<1\), then WSC \(\Leftrightarrow\) \(\mathcal{H}^s(X)>0\).
Proof. By Theorem 3, the WSC implies \(\mathcal{H}^s(X)>0\) for \(s=\dim_{\mathrm{H}}(X)\). This, by Corollary 5, shows that \(X\) is Ahlfors \(s\)-regular. Furthermore, it is easy to see that Ahlfors \(s\)-regularity implies \(\dim_{\mathrm{A}}(X)=s\).
Since \(s<1\), Theorem 4 shows that the WSC is satisfied. ■
Corollary 7.
If \(X \subset \mathbb{R}\) is a self-conformal set and \(\mathcal{H}^s(X)>0\) for \(s=\dim_{\mathrm{H}}(X)\), then the dimension drop conjecture holds.
Proof. In other words, the claim is the following: \(s=P^{-1}(0)\) \(\Leftrightarrow\) there are no exact overlaps.
Recall that, by Corollary 6, WSC \(\Leftrightarrow\) \(\mathcal{H}^s(X)>0\).
If \(s=P^{-1}(0)\) and \(\mathcal{H}^s(X)>0\), then, by Theorem 2, the OSC is satisfied. This immediately shows that there are no exact overlaps.
On the other hand, if the WSC holds and there are no exact overlaps, then the OSC is satisfied. By Theorem 2, the OSC implies \(\mathcal{H}^{P^{-1}(0)}(X)>0\). Since \(\dim_{\mathrm{H}}(X)\le P^{-1}(0)\), we thus have \(s=P^{-1}(0)\). ■