Subadditive ergodic theory and applications
Kingman’s subadditive ergodic theorem
Theorem 1 (Birkhoff (1931)).
Let \(T \colon X \to X\) and \(\mu\) be an ergodic \(T\)-invariant probability measure. If \(f \in L^1(\mu)\), then
\[\lim_{n \to \infty} \tfrac{1}{n} \sum_{k=0}^{n-1} f(T^kx) = \int f \,\mathrm{d}\mu\]
for \(\mu\)-almost all \(x \in X\).
The result can be generalized by recalling the Fekete’s lemma for subadditive sequences \((S_n)_{n \in \mathbb{N}}\): If
\(S_{m+n} \le S_m + S_n\) for all \(m,n \in \mathbb{N}\), then
\(\lim_{n \to \infty} \tfrac{1}{n} S_n = \inf_{n \in \mathbb{N}} \tfrac{1}{n} S_n\).
Theorem 2 (Kingman (1968)).
Let \(T \colon X \to X\) and \(\mu\) be an ergodic \(T\)-invariant probability measure. If \((S_n)_{n \in \mathbb{N}}\) is a subadditive sequence of \(L^1(\mu)\) functions, i.e.
\[S_{m+n} \le S_m + S_n \circ T^m\]
for all \(m,n \in \mathbb{N}\), then
\[\lim_{n \to \infty} \tfrac{1}{n} S_n(x) = \lim_{n \to \infty} \tfrac{1}{n} \int S_n \,\mathrm{d}\mu = \inf_{n \in \mathbb{N}} \tfrac{1}{n} \int S_n \,\mathrm{d}\mu\]
for \(\mu\)-almost all \(x \in X\).
If \(f \in L^1(\mu)\), then choosing \(S_n = \sum_{k=0}^{n-1} f \circ T^k\) the above gives the Birkhoff ergodic theorem.
Norm potential
Consider the semigroup generated by the matrix tuple \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_d(\mathbb{R})^N\).
Let \(\Sigma = \{1,\ldots,N\}^\mathbb{N}\) and if \(\mathtt{i} = i_1i_2\cdots \in \Sigma\), then write \(\mathtt{i}|_n = i_1\cdots i_n\) and \(\Sigma_n = \{\mathtt{i}|_n : \mathtt{i} \in \Sigma\}\) for all \(n \in \mathbb{N}\).
If \(\mathtt{i} \in \Sigma_n\) for some \(n\), then we write \([\mathtt{i}] = \{ \mathtt{j} \in \Sigma : \mathtt{j}|_n = \mathtt{i}\}\).
We use \(\Sigma_* = \bigcup_{n \in \mathbb{N}} \Sigma_n\) to index the elements in the semigroup, that is, \(A_\mathtt{i} = A_{i_1} \cdots A_{i_n}\) for all \(\mathtt{i} = i_1\cdots i_n \in \Sigma_n\) and \(n \in \mathbb{N}\).
Let \(\sigma \colon \Sigma \to \Sigma\), \(\sigma(i_1i_2i_3\cdots) = i_2i_3\cdots\), be the left-shift, \(s>0\), and consider the functions
\[\mathtt{i} \mapsto \log\|A_{\mathtt{i}|_n}\|^s\]
for all \(n \in \mathbb{N}\).
The sequence \(\Phi^s = (\log\|A_{\mathtt{i}|_n}\|^s)_{n \in \mathbb{N}}\) is subadditive.
If \(\mu\) is a \(\sigma\)-invariant Borel probability measure on \(\Sigma\), then the number
\[\lambda(\Phi^s,\mu) = \inf_{n \in \mathbb{N}} \tfrac{1}{n} \sum_{\mathtt{i} \in \Sigma_n} \mu([\mathtt{i}]) \log\|A_\mathtt{i}\|^s = \lim_{n \to \infty} \tfrac{1}{n} \sum_{\mathtt{i} \in \Sigma_n} \mu([\mathtt{i}]) \log\|A_\mathtt{i}\|^s\]
is called the Lyapunov exponent.
If \(\mu\) is ergodic and \(\sigma\)-invariant, then Kingman’s subadditive ergodic theorem implies
\[\lim_{n \to \infty} \tfrac{1}{n} \log\|A_{\mathtt{i}|_n}\| = \lambda(\Phi^1,\mu)\]
for \(\mu\)-almost all \(\mathtt{i} \in \Sigma\).
The existence of the Lyapunov exponent was proved by Furstenberg-Kesten (1960). The number describes the growth rate of \(\|A_{\mathtt{i}|_n}\|\) for a \(\mu\)-generic \(\mathtt{i} \in \Sigma\).
If \(\Psi = (S_n)_{n \in \mathbb{N}}\) is a subadditive sequence of \(L^1(\mu)\) functions, then the pressure of \(\Psi\) is defined by
\[P(\Psi) = \lim_{n \to \infty} \tfrac{1}{n} \log \sum_{\mathtt{i} \in \Sigma_n} \exp\max_{\mathtt{j} \in [\mathtt{i}]} S_n(\mathtt{j}).\]
Recall that the Kolmogorov-Sinai entropy of \(\mu\) is
\[h(\mu) = -\lim_{n \to \infty} \tfrac{1}{n} \sum_{\mathtt{i} \in \Sigma_n} \mu([\mathtt{i}]) \log\mu([\mathtt{i}]).\]
It is easy to see that \(P(\Phi^s) \ge h(\mu) + \lambda(\Phi^s,\mu)\) for all \(\sigma\)-invariant Borel probability measures \(\mu\).
Any \(\sigma\)-invariant Borel probability measure satisfying \(P(\Phi^s) = h(\mu) + \lambda(\Phi^s,\mu)\) is called an equilibrium state for \(\Phi^s\).
Theorem 3 (K (2004)).
There exists an ergodic equilibrium state for \(\Phi^s\).
Let us next determine the structure and properties of equilibrium states for \(\Phi^s\).
Equilibrium states for norm potential
It is remarkable to notice that there can be two distinct ergodic equilibrium states for \(\Phi^s\). For example, let
\[\begin{equation*}
A_1 =
\begin{pmatrix}
\tfrac12 & 0 \\
0 & \tfrac14
\end{pmatrix} \quad \text{and} \quad
A_2 =
\begin{pmatrix}
\tfrac14 & 0 \\
0 & \tfrac12
\end{pmatrix},
\end{equation*}\]
and choose \(s>0\) such that \(2^{-s}+4^{-s}=1\). Then the Bernoulli measures obtained from the probability vectors \((2^{-s},4^{-s})\) and \((4^{-s},2^{-s})\) are both ergodic equilibrium states for \(\Phi^s\).
Theorem 4 (Feng-K (2011)).
If \(s>0\) and \(\mathsf{A} \in \mathrm{GL}_d(\mathbb{R})^N\), then the maximum possible number of distinct ergodic equilibrium states for \(\Phi^s\) is \(d\) and every equilibrium state is fully supported.
A tuple \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_d(\mathbb{R})^N\) is irreducible if there is no non-trivial proper linear subspace \(V\) of \(\mathbb{R}^d\) such that \(A_iV = V\) for all \(i \in \{1,\ldots,N\}\); otherwise \(\mathsf{A}\) is reducible.
A tuple \(\mathsf{A} \in \mathrm{GL}_d(\mathbb{R})^d\) is strongly irreducible if \(V\) above can be replaced by a finite union of non-trivial proper linear subspaces.
The idea of the proof of the previous theorem is to show that the tuple \(\mathsf{A}\) is a tuple of block-upper diagonal matrices in some basis, and then observe that each block in the diagonal is irreducible and contributes one ergodic equilibrium state.
To study the properties of equilibrium states, we may thus assume that the tuple \(\mathsf{A}\) is irreducible.
We say that a Borel probability measure \(\mu\) on \(\Sigma\) is a Gibbs-type measure for \(\Phi^s\) if there exists a constant \(C \ge 1\) such that
\[C^{-1} \le \frac{\mu([\mathtt{i}])}{\exp\bigl( -nP(\Phi^s)) + \log\|A_\mathtt{i}\|^s \bigr)} \le C\]
for all \(\mathtt{i} \in \Sigma_n\) and \(n \in \mathbb{N}\).
Theorem 5 (Feng-K (2011)).
If \(s>0\) and \(\mathsf{A} \in \mathrm{GL}_d(\mathbb{R})^N\) is irreducible, then there is only one equilibrium state for \(\Phi^s\) and it is a Gibbs-type measure for \(\Phi^s\).
Recall that \(A \in \mathrm{GL}_2(\mathbb{R})\) is conformal if there are an invertible conjugation matrix \(M\) and \(c \ne 0\) such that \(cMAM^{-1}\) is an orthogonal matrix. We say that \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is strongly conformal if all the elements of \(\mathsf{A}\) are conformal with respect to the same conjugation matrix.
Let \(\mathbb{RP}^1\) denote the real projective line, which is the set of all lines through the origin in \(\mathbb{R}^2\). We call a proper subset \(\mathcal{C} \subset \mathbb{RP}^1\) a multicone if it is a finite union of closed projective intervals. We say that \(\mathsf{A} \subset \mathrm{GL}_2(\mathbb{R})\) has a strongly invariant multicone if there exists a multicone \(\mathcal{C} \subset \mathbb{RP}^1\) such that \(A\mathcal{C} \subset \mathcal{C}^o\) for all \(A \in \mathsf{A}\).
A Borel probability measure \(\mu\) on \(\Sigma\) is quasi-Bernoulli if there exists a constant \(C \ge 1\) such that
\[C^{-1}\mu([\mathtt{i}])\mu([\mathtt{j}]) \le \mu([\mathtt{i}\mathtt{j}]) \le C\mu([\mathtt{i}])\mu([\mathtt{j}])\]
for all \(\mathtt{i},\mathtt{j} \in \Sigma_*\).
Theorem 6 (Bárány-K-Morris (2018+)).
If \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is irreducible and \(\mu\) is the equilibrium state for \(\Phi^s\), then the following three conditions are equivalent:
(1) \(\mu\) is a quasi-Bernoulli measure,
(2) \(\|A_\mathtt{i} A_\mathtt{j}\| \ge c\|A_\mathtt{i}\|\|A_\mathtt{j}\|\) for all \(\mathtt{i},\mathtt{j} \in \Sigma_*\),
(3) \(\mathsf{A} = \mathsf{A}_e \cup \mathsf{A}_h\), where \(\mathsf{A}_e\) is strongly conformal and \(\mathsf{A}_h\) has a strongly invariant multicone \(\mathcal{C}\) such that \(A\mathcal{C} = \mathcal{C}\) for all \(A \in \mathsf{A}_e\).
Further, let \(f \colon \Sigma \to \mathbb{R}\) be continous and \(\Psi = (\sum_{k=0}^{n-1} f \circ \sigma^k)_{n \in \mathbb{N}}\). Recall that a probability measure \(\mu\) is a Gibbs measure for \(f\) if there exists a constant \(C \ge 1\) such that
\[C^{-1} \le \frac{\mu([\mathtt{i}])}{\exp\bigl( -nP(\Psi) + \sum_{k=0}^{n-1} f(\sigma^k\mathtt{j}) \bigr)} \le C\]
for all \(\mathtt{i} \in \Sigma_n\), \(\mathtt{j} \in [\mathtt{i}]\), and \(n \in \mathbb{N}\).
Theorem 7 (Bárány-K-Morris (2018+)).
If \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is irreducible and \(\mu\) is the equilibrium state for \(\Phi^s\), then the following two conditions are equivalent:
(1) \(\mu\) is a Gibbs measure for a Hölder continuous function,
(2) \(\mathsf{A}\) has a strongly invariant multicone or \(\mathsf{A}\) is strongly conformal.
A Borel probability measure \(\mu\) on \(\Sigma\) is Bernoulli if
\[\mu([\mathtt{i}\mathtt{j}]) = \mu([\mathtt{i}])\mu([\mathtt{j}])\]
for all \(\mathtt{i},\mathtt{j} \in \Sigma_*\). In other words, \(\mu\) is Bernoulli if there exists a probability vector \((p_1,\ldots,p_N)\) such that
\(\mu([\mathtt{i}]) = p_{i_1} \cdots p_{i_n}\)
for all \(\mathtt{i} = i_1\cdots i_n \in \Sigma_n\) and \(n \in \mathbb{N}\).
Theorem 8 (Bárány-K-Morris (2018+)).
If \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is irreducible and \(\mu\) is the equilibrium state for \(\Phi^s\), then the following two conditions are equivalent:
(1) \(\mu\) is a Bernoulli measure,
(2) \(\mathsf{A}\) is strongly conformal.
The picture that emerges is the following:
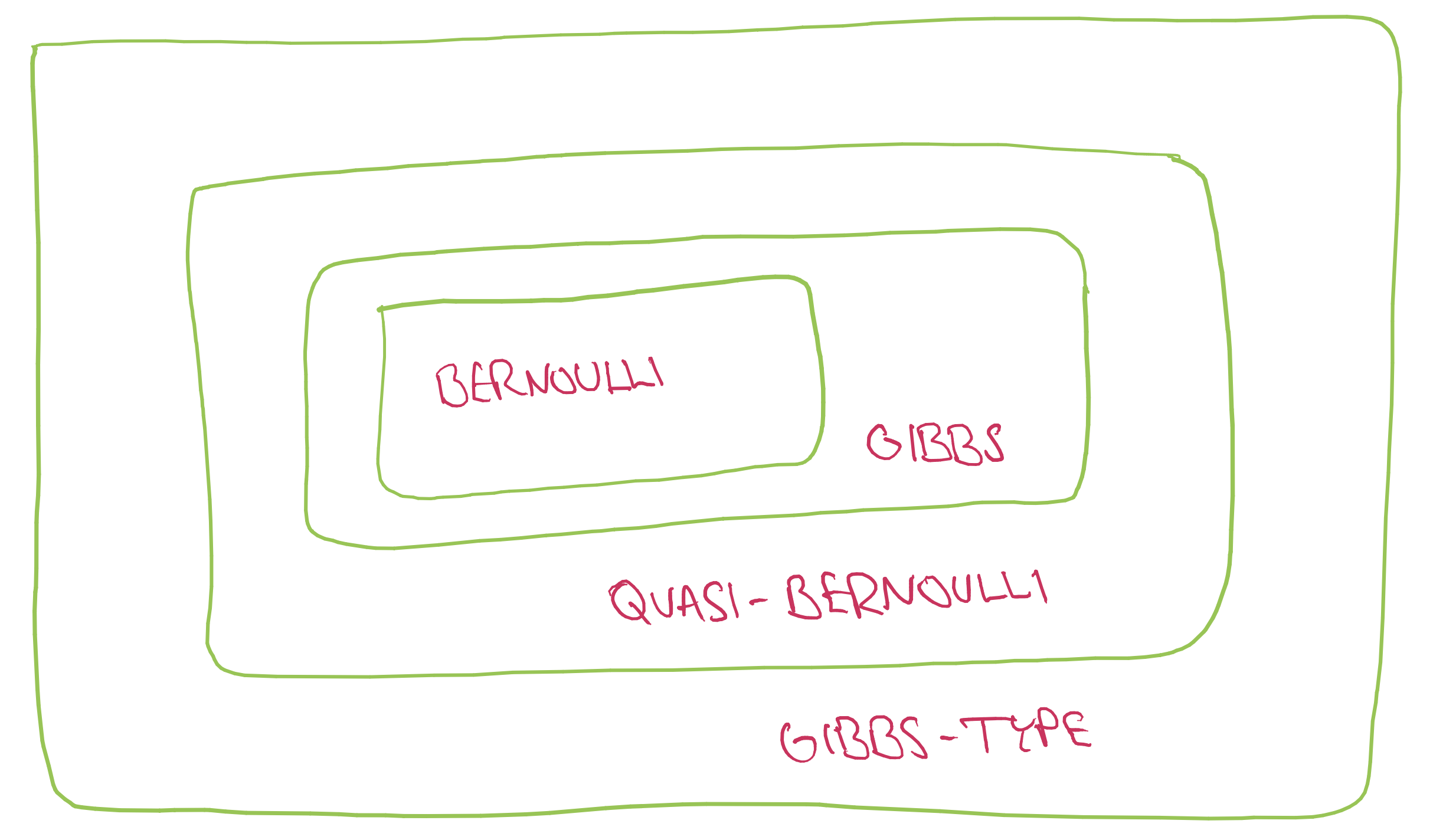
The inclusions can be strict: It can happen that an equilibrium state for \(\Phi^s\) is a Gibbs measure for some Hölder-continuous potential, but is not a Bernoulli measure: Choose two positive matrices
\[\begin{equation*}
A_1 =
\begin{pmatrix}
2 & 1 \\
1 & 1
\end{pmatrix}
\quad\text{and}\quad
A_2 =
\begin{pmatrix}
2 & 1 \\
1 & 2
\end{pmatrix}.
\end{equation*}\]
Then Theorem 7 and Theorem 8 give the claim as \((A_1,A_2)\) is irreducible and has a strongly invariant multicone (i.e. the union of the first and third quadrants).
Furthermore, it is possible that an equilibrium state for \(\Phi^s\) is a quasi-Bernoulli measure, but is not a Gibbs measure for any Hölder-continuous potential: Let \(A_1\) and \(A_2\) be as above. Then Theorem 6 and Theorem 7 verify this as \((A_1,A_2,I)\) is irreducible and has an invariant multicone (i.e. the union of the first and third quadrants).
Finally, it can happen that an equilibrium state for \(\Phi^s\) is a Gibbs-type measure for \(\Phi^s\), but is not a quasi-Bernoulli measure: Choose two matrices
\[\begin{equation*}
A_3 =
\begin{pmatrix}
1 & 0 \\
0 & 2
\end{pmatrix}
\quad\text{and}\quad
A_4 =
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}.
\end{equation*}\]
Then Theorem 5 and Theorem 6 give the claim as \((A_3,A_4)\) is irreducible, has no invariant multicone, and does not contain only conformal matrices.
Equilibrium states for singular value function
Recall that the singular values \(\|A\| = \alpha_1(A) \ge \cdots \ge \alpha_d(A) > 0\) of \(A \in \mathrm{GL}_d(\mathbb{R})\) are the square roots of the non-negative real eigenvalues of the positive semidefinite matrix \(A^\top A\).
If \(0 \le s \le d\) and \(k\le s < k+1\), then the singular value function of \(A \in \mathrm{GL}_d(\mathbb{R})\) with parameter \(s\) is
\[\varphi^s(A) = \|A^{\wedge k}\|^{k+1-s} \|A^{\wedge(k+1)}\|^{s-k} = \alpha_1(A) \cdots \alpha_k(A) \alpha_{k+1}(A)^{s-k}.\]
It follows that \(\varphi^s(AB) \le \varphi^s(A)\varphi^s(B)\) for all \(A,B \in \mathrm{GL}_d(\mathbb{R})\), and hence, the sequence \(\hat \Phi^s = (\log\varphi^s(A_{\mathtt{i}|_n}))_{n \in \mathbb{N}}\) is subadditive.
If \(\mu\) is a \(\sigma\)-invariant Borel probability measure on \(\Sigma\), then the number
\[\lambda(\hat\Phi^s,\mu) = \inf_{n \in \mathbb{N}} \tfrac{1}{n} \sum_{\mathtt{i} \in \Sigma_n} \mu([\mathtt{i}]) \log\varphi^s(A_\mathtt{i}) = \lim_{n \to \infty} \tfrac{1}{n} \sum_{\mathtt{i} \in \Sigma_n} \mu([\mathtt{i}]) \log\varphi^s(A_\mathtt{i})\]
is called the generalized Lyapunov exponent.
If \(\mu\) is ergodic and \(\sigma\)-invariant, then Kingman’s subadditive ergodic theorem implies
\[\lim_{n \to \infty} \tfrac{1}{n} \log\varphi^s(A_{\mathtt{i}|_n}) = \lambda(\hat\Phi^s,\mu)\]
for \(\mu\)-almost all \(\mathtt{i} \in \Sigma\). It is again easy to see that \(P(\hat\Phi^s) \ge h(\mu) + \lambda(\hat\Phi^s,\mu)\)
for all \(\sigma\)-invariant Borel probability measures \(\mu\).
Any \(\sigma\)-invariant Borel probability measure satisfying \(P(\hat\Phi^s) = h(\mu) + \lambda(\hat\Phi^s,\mu)\)
is called an equilibrium state for \(\hat\Phi^s\).
The result of K (2004) guarantees the existence of an ergodic equilibrium state also in this case.
Furthermore, note that all the previous results hold for \(\hat\Phi^s\) when \(d=2\) since
\[\varphi^s(A) =
\begin{cases}
\|A\|^s, &\text{if } 0<s<1, \\
|\det(A)|^{s-(d-1)} \|A^{\wedge(d-1)}\|^{d-s}, &\text{if } d-1<s<d.
\end{cases}\]
Theorem 9 (Feng-K (2011)).
If \(0 < s < 2\) and \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})\), then the maximum possible number of distinct ergodic equilibrium states for \(\hat\Phi^s\) is \(2\) and every equilibrium state is fully supported.
Theorem 10 (K-Morris (2018)).
If \(0 < s < 3\) and \(\mathsf{A} \in \mathrm{GL}_3(\mathbb{R})^N\), then the maximum possible number of distinct ergodic equilibrium states for \(\hat\Phi^s\) is \(6\), if \(1 < s <2\), and \(3\), if otherwise, and every equilibrium state is fully supported.
If \(s \in (0,1) \cup (2,3)\), then the above result follows from Feng-K (2011). The case \(1<s<2\) divides into three further subcases which are all studied by completely different methods.
Theorem 11 (Bochi-Morris (2017+)).
If \(0 < s < d\) and \(\mathsf{A} \in \mathrm{GL}_d(\mathbb{R})^N\), then there are at most finitely many distinct ergodic equilibrium states for \(\hat\Phi^s\), and every equilibrium state is fully supported.
Bochi-Morris (2017+) found an upper bound \(\binom{d}{\lfloor s \rfloor}\binom{d}{\lceil s \rceil}\) which is unlikely sharp. In K-Morris (2018), we conjectured that the maximum possible number of distinct ergodic equilibrium states for \(\Phi^s\) is \((d-\lfloor s \rfloor)\binom{d}{\lfloor s \rfloor}\). The following result shows that topologically and measure-theoretically generic matrix tuples define a unique equilibrium state.
Theorem 12 (K-Li (2017)).
The set \(\{\mathsf{A} \in \mathrm{GL}_d(\mathbb{R})^N :\) equilibrium state for \(\hat\Phi^s\) is not unique\(\}\) is contained in a finite union of \((d^2N-1)\)-dimensional algebraic varieties.
Dimension theory of self-affine sets
If \(f_1,\ldots,f_N \colon \mathbb{R}^d \to \mathbb{R}^d\) are affine, i.e. \(f_i(x) = A_ix+v_i\), where \(A_i \in \mathrm{GL}_d(\mathbb{R})\) and \(v_i \in \mathbb{R}^d\), then the tuple \((f_1,\ldots,f_N)\) is called an affine IFS. It is a classical result that there exists a nonempty compact set \(X \subset \mathbb{R}^d\) such that
\[X = \bigcup_{i=1}^N f_i(X).\]
A central problem is to calculate or estimate the dimension of the self-affine set \(X\).
In the special case, where each \(A_i\) is a scalar multiple of an isometry, i.e. \(f_i(x) = r_iO_ix+v_i\),
then \((f_1,\ldots,f_N)\) is called a similarity IFS and the set \(X\) self-similar.
IFSs can be considered to be idealized models for fractal sets.
From the analysis point of view, IFSs are used to produce counter-examples and to study sharpness of results.
For example, Bonk-Merenkov (2013) showed that quasisymmetric maps between two Sierpiński carpets are isometries.
Jordan-Sahlsten (2016) solved Salem’s problem by using IFSs.
If \((f_1,\ldots,f_N)\) is a similitude IFS satisfying the SSC (i.e. \(f_i(X) \cap f_j(X) = \emptyset\) for \(i \ne j\)), then it is a classical result that
\[\dim_{\mathrm{H}}(X) = s,\]
where \(\sum_{i=1}^N r_i^s = 1\) or, equivalently, \(P(\Phi^s)=0\), where \(\Phi^s = (\log r_{\mathtt{i}|_n}^s)_{n \in \mathbb{N}}\) and \(r_{\mathtt{i}|_n} = r_{i_1} \cdots r_{i_n}\) for all \(\mathtt{i} = i_1 i_2 \cdots \in \Sigma\).
Without separation the question is difficult. Write \(f_\mathtt{i} = f_{i_1} \circ \cdots \circ f_{i_n}\) for all \(\mathtt{i} = i_1 \cdots i_n \in \Sigma_n\) and \(n \in \mathbb{N}\), and say that \(X\) has exact overlaps if \(f_\mathtt{i} = f_\mathtt{j}\) for some \(\mathtt{i} \ne \mathtt{j}\).
Theorem 13 (Hochman (2014)).
If the similarity IFS in the real line is defined by algebraic parameters, then the associated self-similar set \(X\) either has exact overlaps or \(\dim_{\mathrm{H}}(X) = \min\{1,s\}\), where \(P(\Phi^s)=0\).
Although it is easy to find affine IFSs \((f_1,\ldots,f_N)\) satisfying the SSC such that \(\dim_{\mathrm{H}}(X) < s\), where \(P(\hat\Phi^s)=0\), it is still expected that this \(s\), denoted by \(\dim_{\mathrm{aff}}(\mathsf{A})\), gives the dimension for a large class of self-affine sets.
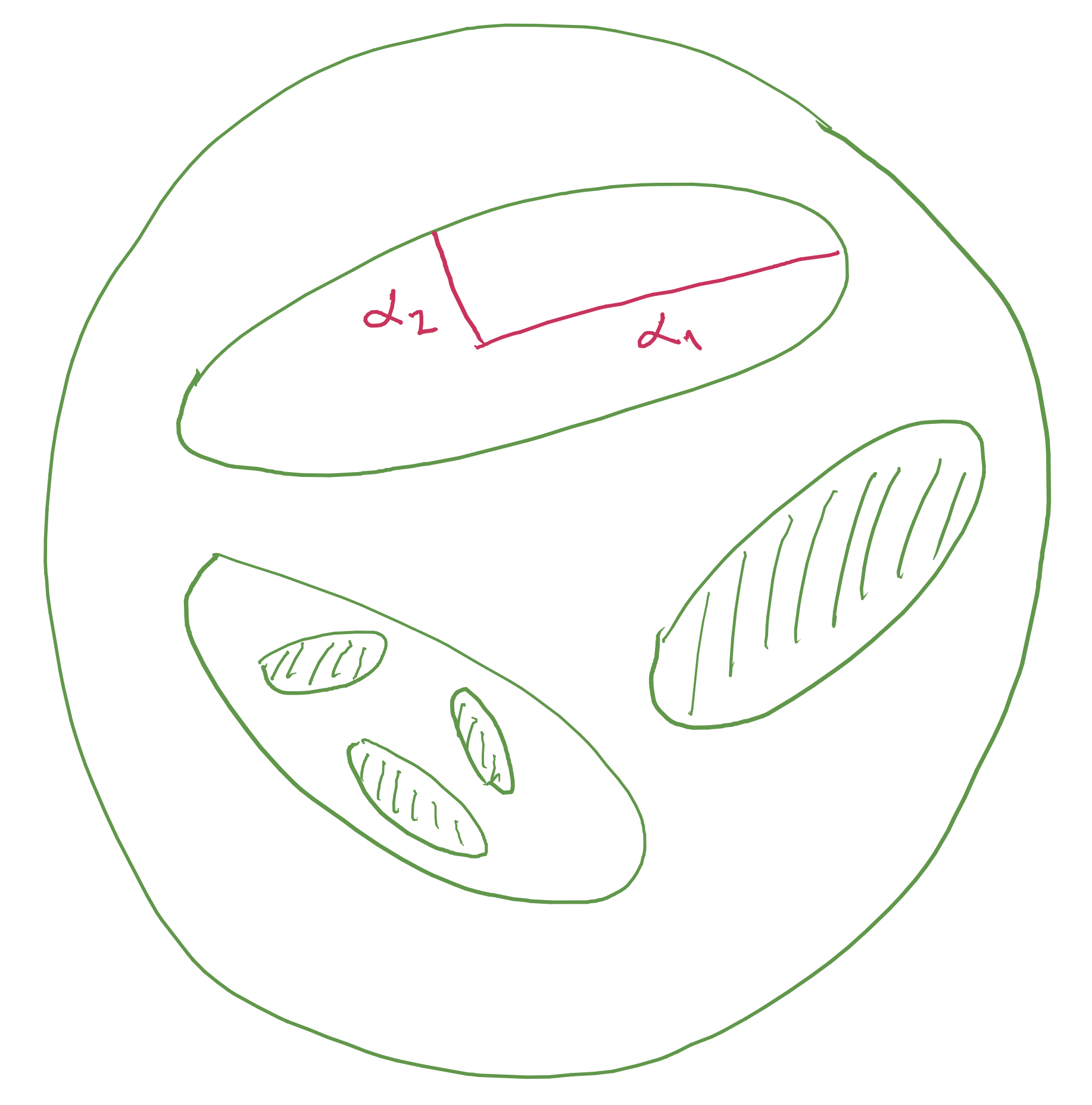
Recall that the singular value \(\alpha_i(A)\) is the length of the \(i\)th semiaxis of \(A(B(0,1))\).
Intuitively, \(\varphi^s(A)\) represents a measurement of the \(s\)-dimensional volume of the image of the unit ball under \(A\).
For example, if \(d=2\) and \(1 \le s < 2\), then
\[\varphi^s(A) = \alpha_1(A) \alpha_2(A)^{s-1} = \frac{\alpha_1(A)}{\alpha_2(A)} \alpha_2(A)^s,\]
where \(\frac{\alpha_1(A)}{\alpha_2(A)}\) roughly tells how many balls of radius \(\alpha_2(A)\) are needed to cover \(A(B(0,1))\),
and we have
\[\mathcal{H}^s(X) \lesssim \lim_{n \to \infty} \sum_{\mathtt{i} \in \Sigma_n} \frac{\alpha_1(A_\mathtt{i})}{\alpha_2(A_\mathtt{i})} \alpha_2(A_\mathtt{i})^s.\]
Since
\[P(\hat\Phi^s) = \lim_{n \to \infty} \tfrac{1}{n} \log \sum_{\mathtt{i} \in \Sigma_n} \frac{\alpha_1(A_\mathtt{i})}{\alpha_2(A_\mathtt{i})} \alpha_2(A_\mathtt{i})^s\]
is strictly decreasing in \(s\), we see that \(\dim_{\mathrm{H}}(X) \le \dim_{\mathrm{aff}}(\mathsf{A})\).
If \(\dim_{\mathrm{H}}(X) < \dim_{\mathrm{aff}}(\mathsf{A})\), then the covers obtained from the ellipses are not optimal:
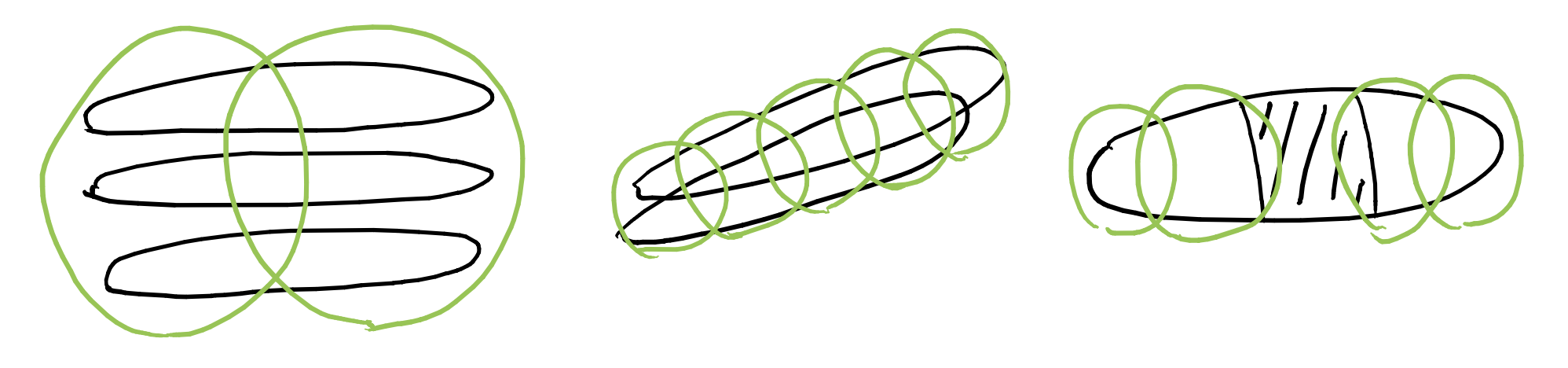
Thus far the dimension theory of self-affine sets has focused on specific subclasses. The problem of finding the dimension can be make more tractable either by assuming some randomness in the defining IFS or by imposing special relations between the affine maps.
Let \(\pi \colon \Sigma \to X\) be the canonical projection defined by \(\pi(i_1i_2\cdots) = \sum_{k=1}^\infty A_{i_1}\cdots A_{i_{k-1}}v_{i_k}\).
If \(\mu\) is a Bernoulli measure on \(\Sigma\), then the push-forward measure \(\pi_*\mu\) is called self-affine.
We say that a Borel probability measure \(\mu\) on \(\mathbb{R}^d\) is exact-dimensional if there exists \(s \ge 0\) such that
\[\exists \lim_{r \downarrow 0} \frac{\log\mu(B(x,r))}{\log r} = s\]
for \(\mu\)-almost all \(x \in \mathbb{R}^d\). The following result is valid for all planar self-affine sets.
Theorem 14 (Bárány-K (2017)).
If \(\mu\) is a self-affine measure on a self-affine set \(X\), then \(\mu\) is exact-dimensional and satisfies the so-called Ledrappier-Young formula.
A classical dimension result for self-affine sets is due to Falconer. It guarantees that for a random choice of translation vectors the covers are optimal.
We write \(X_{\mathsf{A},\mathsf{v}}\) to emphasize the dependence of the self-affine set \(X\) on the matrices \(\mathsf{A} = (A_1,\ldots,A_N)\) and the translation vectors \(\mathsf{v} = (v_1,\ldots,v_N)\).
Theorem 15 (Falconer (1988)).
If \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathrm{GL}_d(\mathbb{R})^N\) satisfies \(\| A_i \| < 1/2\) for all \(i\), then
\[\dim_{\mathrm{H}}(X_{\mathsf{A},\mathsf{v}}) = \dim_{\mathrm{aff}}(\mathsf{A})\]
for \(\mathcal{L}^{dN}\)-almost all \(\mathsf{v} = (v_1,\ldots,v_N) \in (\mathbb{R}^d)^N\).
The proof of the result follows from the existence of an equilibrium state for \(\hat\Phi^s\) and a transversality argument.
Let \(\mathcal{A}_{\mathsf{v}} \subset \mathrm{GL}_2(\mathbb{R})^N\) be the collection of matrix tuples satisfying the following:
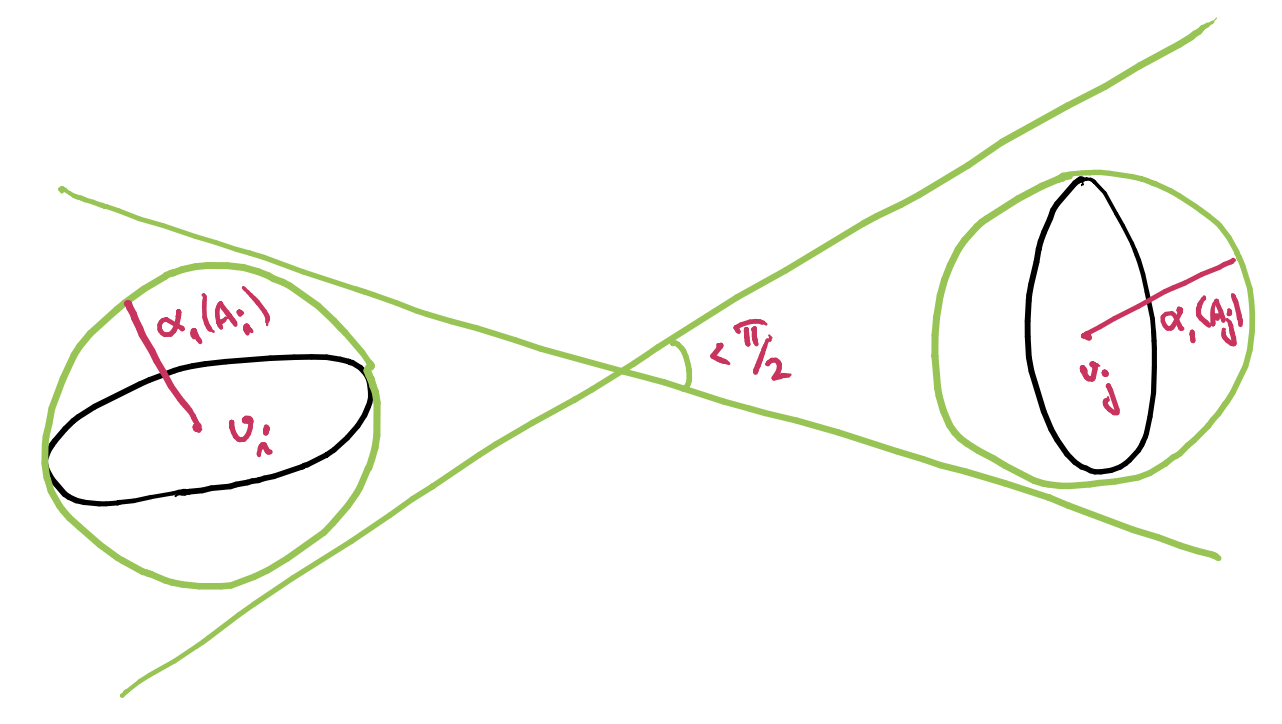
Relying also on the Ledrappier-Young formula, we managed to show an orthogonal version for Falconer’s result.
Theorem 16 (Bárány-K-Koivusalo (2018)).
If \(\mathsf{v} = (v_1,\ldots,v_N) \in (\mathbb{R}^d)^N\) is such that \(v_i \ne v_j\) for \(i \ne j\), then
\[\dim_{\mathrm{H}}(X_{\mathsf{A},\mathsf{v}}) = \dim_{\mathrm{aff}}(\mathsf{A})\]
for \(\mathcal{L}^{d^2N}\)-almost all \(\mathsf{A} = (A_1,\ldots,A_N) \in \mathcal{A}_{\mathsf{v}} \subset \mathrm{GL}_d(\mathbb{R})^N\).
In the plane, the following theorem generalizes Theorem 16.
Theorem 17 (Bárány-Hochman-Rapaport (2017+)).
If \((f_1,\ldots,f_N)\) is a planar affine IFS satisfying the SSC such that the associated matrix tuple \(\mathsf{A} \in \mathrm{GL}_2(\mathbb{R})^N\) is proximal and strongly irreducible, then
\[\dim_{\mathrm{H}}(X_{\mathsf{A},\mathsf{v}}) = \dim_{\mathrm{aff}}(\mathsf{A}).\]
Very roughly speaking, the proof relies on Hochman’s dimension result Theorem 13 for self-similar sets in the real line, the Ledrappier-Young formula of Theorem 14, and the existence of an equilibrium state for \(\hat\Phi^s\) given by Theorem 3.
Open questions
Does \(\dim_{\mathrm{H}}(X_{\mathsf{A},\mathsf{v}}) = \dim_{\mathrm{aff}}(\textsf{A})\) hold without the SSC for strongly irreducible matrix tuples? What about higher dimensions? What can be said about countable systems? Recall that equilibrium states are fully supported. Relying on this and the definition of the equilibrium state, it is easy to see that if \(\mathsf{A} = (A_1\ldots,A_N) \in \mathrm{GL}_d(\mathbb{R})^N\) and \(\mathsf{A}' = (A_1\ldots,A_{N-1})\), then
\[\dim_{\mathrm{aff}}(\mathsf{A}') < \dim_{\mathrm{aff}}(\mathsf{A}).\]
Is \(\dim_{\mathrm{H}}(X_{\mathsf{A}',\mathsf{v}'}) < \dim_{\mathrm{H}}(X_{\mathsf{A},\mathsf{v}})\) for all \(\mathsf{A}\) and \(\mathsf{v}\)?
What is the Assouad dimension of the self-affine set?
Is it possible to do multifractal analysis on self-affine sets, in particular, for local dimension?
What can be said about dimension theory of non-conformal and non-affine systems?