Super-exponential condensation without exact overlaps

December 3, 2020

Self-similar sets

A tuple \(\Phi = (\varphi_1,\ldots,\varphi_N)\) of contractive similarities \(\varphi_i \colon \mathbb{R} \to \mathbb{R}\), \(\varphi_i(x) = \lambda_i x + t_i\), where \(0<|\lambda_i|<1\) is the contraction and \(t_i \in \mathbb{R}\) is the translation, is called a similarity iterated function system (IFS). For each similarity IFS \(\Phi\) there exists unique nonempty compact set \(X \subset \mathbb{R}^d\), the self-similar set, for which

\[X = \bigcup_{i=1}^N \varphi_i(X).\]

A point \(x \in \mathbb{R}\) belongs to \(X\) if and only if there exists \(\mathtt{i} = i_1i_2\cdots\) such that \(\lim_{n \to \infty} \varphi_{\mathtt{i}|_n}(0) = x\). We write \(\varphi_\mathtt{i} = \varphi_{i_1} \circ \cdots \circ \varphi_{i_n}\), \(\lambda_\mathtt{i} = \lambda_{i_1} \cdots \lambda_{i_n}\), and \(|\mathtt{i}|=n\) for all \(\mathtt{i} = i_1 \cdots i_n\). We have \(\dim_{\mathrm{H}}(X) \le \dim_{\mathrm{sim}}(X)\), where the similarity dimension \(\dim_{\mathrm{sim}}(X)\) is the unique \(s \ge 0\) for which \(\sum_{i=1}^N |\lambda_i|^s = 1\). If the strong separation condition is satisfied, which means that \(\varphi_i(X) \cap \varphi_j(X) = \emptyset\) whenever \(i \ne j\), then \(\dim_{\mathrm{H}}(X) = \dim_{\mathrm{sim}}(X)\).

The strong separation condition above can be relaxed to the open set condition which allows “slight overlaps”. We say that \(X\) has exact overlaps, if there are finite sequences \(\mathtt{i} \ne \mathtt{j}\) such that \(\varphi_\mathtt{i} = \varphi_\mathtt{j}\). If \(\mathtt{i}\) and \(\mathtt{j}\) have different length, then we may replace them by the same length words \(\mathtt{i}\mathtt{j}\) and \(\mathtt{j}\mathtt{i}\).

Lemma 1. If a self-similar set \(X\) has exact overlaps, then \(\dim_{\mathrm{H}}(X) < \dim_{\mathrm{sim}}(X)\).

Proof. Since

\[\sum_{\genfrac{}{}{0pt}{}{|\mathtt{i}|=n}{\mathtt{i} \ne \mathtt{j}}} |\lambda_\mathtt{i}|^s < \sum_{|\mathtt{i}|=n} |\lambda_\mathtt{i}|^s = \bigl( \sum_{i=1}^N |\lambda_i|^s \bigr)^n = 1 = \sum_{i=1}^N |\lambda_i|^s,\]

the claim follows. ■

For self-similar sets in the real line with \(\dim_{\mathrm{sim}}(X) \le 1\), no other mechanism is known which drops the dimension of \(X\) below the similarity dimension.

Dimension drop conjecture

The following conjecture, also known as the exact overlapping conjecture, is probably the most well-known open problem in fractal geometry.

Dimension drop conjecture. If \(X \subset \mathbb{R}\) is a self-similar set such that \(\dim_{\mathrm{H}}(X) < \min\{1,\dim_{\mathrm{sim}}(X)\}\), then \(X\) has exact overlaps.

The quantity \(\Delta_n = \min\{|\varphi_\mathtt{i}(0)-\varphi_\mathtt{j}(0)| : \mathtt{i} \ne \mathtt{j}\) have length \(n\) and \(\lambda_\mathtt{i}=\lambda_\mathtt{j}\}\) is zero for arbitrary large \(n\) if and only if there is an exact overlap. It is also easy to see that \(\Delta_n \to 0\) at least exponentially. We say that a self-similar set \(X\) is exponentially separated if there is \(c>0\) such that \(\Delta_n \ge c^n\) for arbitrary large \(n\) and super-exponentially condensated if \(\lim_{n \to \infty} \tfrac{1}{n}\log\Delta_n = -\infty\).

Theorem 2 (Hochman (2014)). If \(\dim_{\mathrm{H}}(X) < \min\{1,\dim_{\mathrm{sim}}(X)\}\), then \(X\) is super-exponentially condensated.

If \(X\) is defined by using algebraic parameters in the IFS and there are no exact overlaps, then a lemma of Garcia (1962) implies that \(X\) is exponentially separated and Theorem 2 shows that \(\dim_{\mathrm{H}}(X) = \min\{1,\dim_{\mathrm{sim}}(X)\}\), i.e. there is no dimension drop. Rapaport (2020+) improved this observation by proving that it suffices to assume only the contraction ratios \(\lambda_i\) to be algebraic. In his ICM talk in 2018, Hochman asked if there exist super-exponentially condensated self-similar sets without exact overlaps? If such sets did not exist, then Theorem 2 would settle the dimension drop conjecture. Unfortunately (or fortunately) this is not the case:

Theorem 3 (Baker (2019+) and Bárány-K (2019+)). There exist super-exponentially condensated self-similar sets without exact overlaps.

Since the contractions in Baker’s example are rational numbers, Rapaport (2020+) was able to apply his result to show the existence of a super-exponentially condensated self-similar set having no dimension drop.

Self-similar measures and Bernoulli convolutions

Dimension drop conjecture can also be formulated for measures. Let \(p = (p_1,\ldots,p_N)\) be a probability vector with \(p_i>0\). There exists a unique Borel probability measure \(\mu\) on \(\mathbb{R}\) such that

\[\mu = \sum_{i=1}^N p_i \mu \circ \varphi_i^{-1}.\]

The measure \(\mu\) is called self-similar measure and its support is the self-similar set \(X\). A famous example of self-similar measure is the family of Bernoulli convolutions \(\{\mu_\lambda\}_{\lambda \in (0,1)}\) which are defined by the similarity IFS \(\Phi^\lambda\) consisting of functions \(\varphi_1(x)=\lambda x-1\) and \(\varphi_2(x)=\lambda x+1\), and the probability vector \((\tfrac12,\tfrac12)\). In other words, the Bernoulli convolution \(\mu_\lambda\) is the distribution of the random sum \(\sum_{n=0}^\infty \pm\lambda^n\). A Borel probability measure \(\mu\) on \(\mathbb{R}\) is exact dimensional if there exists \(s \ge 0\) such that

\[\lim_{r \downarrow 0} \frac{\log\mu([x-r,x+r])}{\log r} = s\]

for \(\mu\)-almost all \(x \in \mathbb{R}\).

Theorem 4 (Feng-Hu (2009)). Self-similar measures are exact dimensional.

The value \(s\) above is the dimension of \(\mu\) and we write \(\dim(\mu)=s\). It is sufficiently easy to see that \(\dim(\mu) = \inf\{\dim_{\mathrm{H}}(A) : \mu(A)>0\} \le \dim_{\mathrm{H}}(X).\) Let us define the Lyapunov dimension of a self-similar measure \(\mu\) by

\[\dim_{\mathrm{L}}(\mu) = \frac{\sum_{i=1}^N p_i\log p_i}{\sum_{i=1}^N p_i\log \lambda_i}.\]

We always have \(\dim(\mu) \le \dim_{\mathrm{L}}(\mu) \le \dim_{\mathrm{sim}}(X)\) and if the strong separation condition is satisfied, then \(\dim(\mu) = \dim_{\mathrm{L}}(\mu)\).

Theorem 5 (Jordan-Pollicott-Simon (2007)). For fixed \(\mu\) and \(\lambda_i\)’s, \(\dim(\mu) = \min\{1,\dim_{\mathrm{L}}(\mu)\}\) holds for Lebesgue almost all translation vectors \(t_i\).

Dimension drop conjecture. If \(\mu\) is a self-similar measure such that \(\dim(\mu) < \min\{1,\dim_{\mathrm{L}}(\mu)\}\), then \(X\) has exact overlaps.

The equilibrium state, i.e. the shift-invariant measure \(\mu\) for which \(\dim_{\mathrm{L}}(\mu)=\dim_{\mathrm{sim}}(X)\), is a self-similar measure. Therefore, if there is a dimension drop for \(X\), then

\[\dim(\mu) \le \dim_{\mathrm{H}}(X) < \dim_{\mathrm{sim}}(X) = \dim_{\mathrm{L}}(\mu)\]

and there is a dimension drop for \(\mu\). Kempton has proposed the following question: Does \(\dim_{\mathrm{H}}(X)<\min\{1,\dim_{\mathrm{sim}}(X)\}\) if and only if \(\dim(\mu)<\min\{1,\dim_{\mathrm{L}}(\mu)\}\) for all self-similar measures \(\mu\)? For Bernoulli convolutions, it is easy to calculate that

\[\dim_{\mathrm{L}}(\mu_\lambda) = \frac{\log \frac12}{\log\lambda}.\]

If \(\lambda \in (0,\tfrac12)\), then the strong separation condition holds and there is no dimension drop. Erdős (1939) has shown that \(\dim(\mu_\lambda)<1\) when \(\lambda \in (\tfrac12,1)\) is an inverse of a Pisot number. Solomyak (1995) proved that the measure \(\mu_\lambda\) is absolutely continuous for Lebesgue almost all \(\lambda \in (\tfrac12,1)\). Shmerkin (2014) improved this by showing that the measure \(\mu_\lambda\) is absolutely continuous outside of Hausdorff dimension zero set. Finally, Varjú (2019) managed to prove that \(\dim(\mu_\lambda)=1\) for every transcendental \(\lambda \in (\tfrac12,1)\). Together with Theorem 2, which holds also for self-similar measures, Varjú’s theorem verifies the dimension drop conjecture for Bernoulli convolutions.

Projection of Sierpiński triangle

Let us next consider the following parametrized IFS \(\Phi^{\lambda,t}\):

\[\varphi_1^{\lambda,t}(x) = \lambda x, \quad \varphi_2^{\lambda,t}(x) = \lambda x + t, \quad \varphi_3^{\lambda,t}(x) = \lambda x + 1.\]

The IFS \(\Phi^{\frac13,t}\) appears as a projection of the Sierpiński triangle. Furstenberg (1970) conjectured that if the one-dimensional Sierpiński triangle is projected orthogonally to a line of irrational slope, then the dimension of the image is \(1\). Hochman (2014) gave an affirmative answer to this conjecture. Let us define three sets for \(\Phi^{\lambda,t}\). The exact overlapping set is

\[\mathcal{E} = \{(\lambda,t) \in \mathbb{R}^2 : \varphi_\mathtt{i}^{\lambda,t}=\varphi_\mathtt{j}^{\lambda,t} \text{ for some finite sequences } \mathtt{i}\ne\mathtt{j}\},\]

the dimension drop set is

\[\mathcal{D} = \{(\lambda,t) \in \mathbb{R}^2 : \dim_{\mathrm{H}}(X^{\lambda,t})<\dim_{\mathrm{sim}}(X^{\lambda,t})=-\log 3/\log\lambda\},\]

and the super-exponential condensation set is

\[\mathcal{C} = \{(\lambda,t) \in \mathbb{R}^2 : \lim_{n\to\infty}\tfrac{1}{n}\log\Delta_n^{\lambda,t}=-\infty\}.\]

Lemma 1 shows that \(\mathcal{E} \subset \mathcal{D}\) and Theorem 2 verifies that \(\mathcal{D} \subset \mathcal{C}\). For \(\Phi^{\lambda,t}\), the dimension drop conjecture is equivalent to \(\mathcal{D} \setminus \mathcal{E} = \emptyset\).

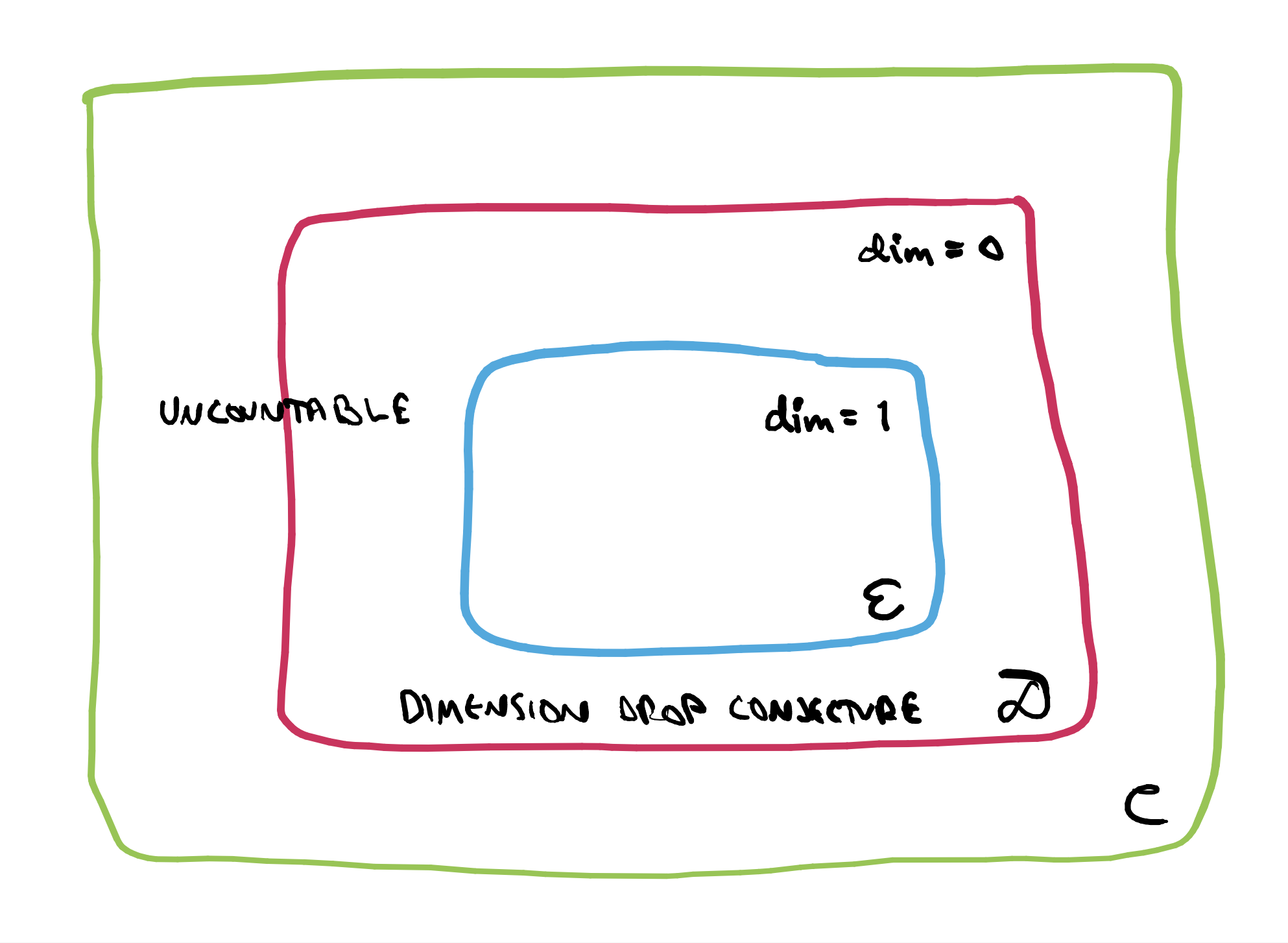
Furthermore, it follows from Hochman (2015+) that \(\dim_{\mathrm{H}}(\mathcal{E})=1=\dim_{\mathrm{p}}(\mathcal{C})\) and from Rapaport-Varjú (2020+) that \(\dim_{\mathrm{H}}(\mathcal{D} \setminus \mathcal{E})=0\). Theorem 3 follows from the following result:

Theorem 6 (Bárány-K (2019+)). The set \(\mathcal{C} \setminus \mathcal{E}\) is uncountable.

Proof. Let us sketch the main idea in the proof. How to show that \(\mathcal{C} \setminus \mathcal{E} \ne \emptyset\)? Note that if \(\varphi_i(X) \cap \varphi_j(X) \ne \emptyset\), then \(i=1\) and \(j=2\). We also have

\[\varphi_\mathtt{i}^{\lambda,t}(0) = \sum_{k=1}^n (\delta_{i_k}^3+t\delta_{i_k}^2)\lambda^{k-1}\]

for all \(\mathtt{i} = i_1\cdots i_n\), where

\[\begin{equation*} \delta_i^j = \begin{cases} 1, &\text{if } i=j, \\ 0, &\text{if } i\ne j. \end{cases} \end{equation*}\]

Lemma 7. If \(\mathtt{i}=i_1\cdots i_n\) and \(\mathtt{j}=j_1\cdots j_n\) are such that \(i_1 \ne j_1\), then

\[|\varphi_\mathtt{i}^{\lambda,t}(0) - \varphi_\mathtt{j}^{\lambda,t}(0)| < \varepsilon \quad\Longleftrightarrow\quad \biggl| t - \frac{\sum_{k=1}^n (\delta_{j_k}^3-\delta_{i_k}^3)\lambda^{k-1}}{\sum_{k=1}^n (\delta_{i_k}^2-\delta_{j_k}^2)\lambda^{k-1}} \biggr| < \varepsilon'.\]

Define a non-linear projection by

\[\mathrm{proj}(x,y) = \frac{x}{y}\]

and let us express the ratio

\[\frac{\sum_{k=1}^n (\delta_{j_k}^3-\delta_{i_k}^3)\lambda^{k-1}}{\sum_{k=1}^n (\delta_{i_k}^2-\delta_{j_k}^2)\lambda^{k-1}}\]

by using the projection: Write \(\beta(i,j) = (\delta_j^3-\delta_i^3,\delta_i^2-\delta_j^2)\) and extend it to sequences by \(\beta(\mathtt{i},\mathtt{j}) = \beta(i_1,j_1)\cdots\beta(i_n,j_n)\). If \(S_{(i,j)}^\lambda(x,y) = (\lambda x+i,\lambda y+j)\), then Lemma 7 gives:

Lemma 8. If \(\mathtt{i} \ne \mathtt{j}\), then

\[|\varphi_\mathtt{i}^{\lambda,t}(0) - \varphi_\mathtt{j}^{\lambda,t}(0)| < \varepsilon \quad\Longleftrightarrow\quad |t - \mathrm{proj}(S_{\beta(\mathtt{i},\mathtt{j})}^\lambda(0,0))| < \lambda^{-|\mathtt{i} \land \mathtt{j}|} \varepsilon'\]

Therefore, in order to achieve super-exponential condensation, the parameter \(t\) must be contained in a super-exponential neighbourhood of \(\mathrm{proj}(S_{\beta(\mathtt{i},\mathtt{j})}^\lambda(0,0))\).

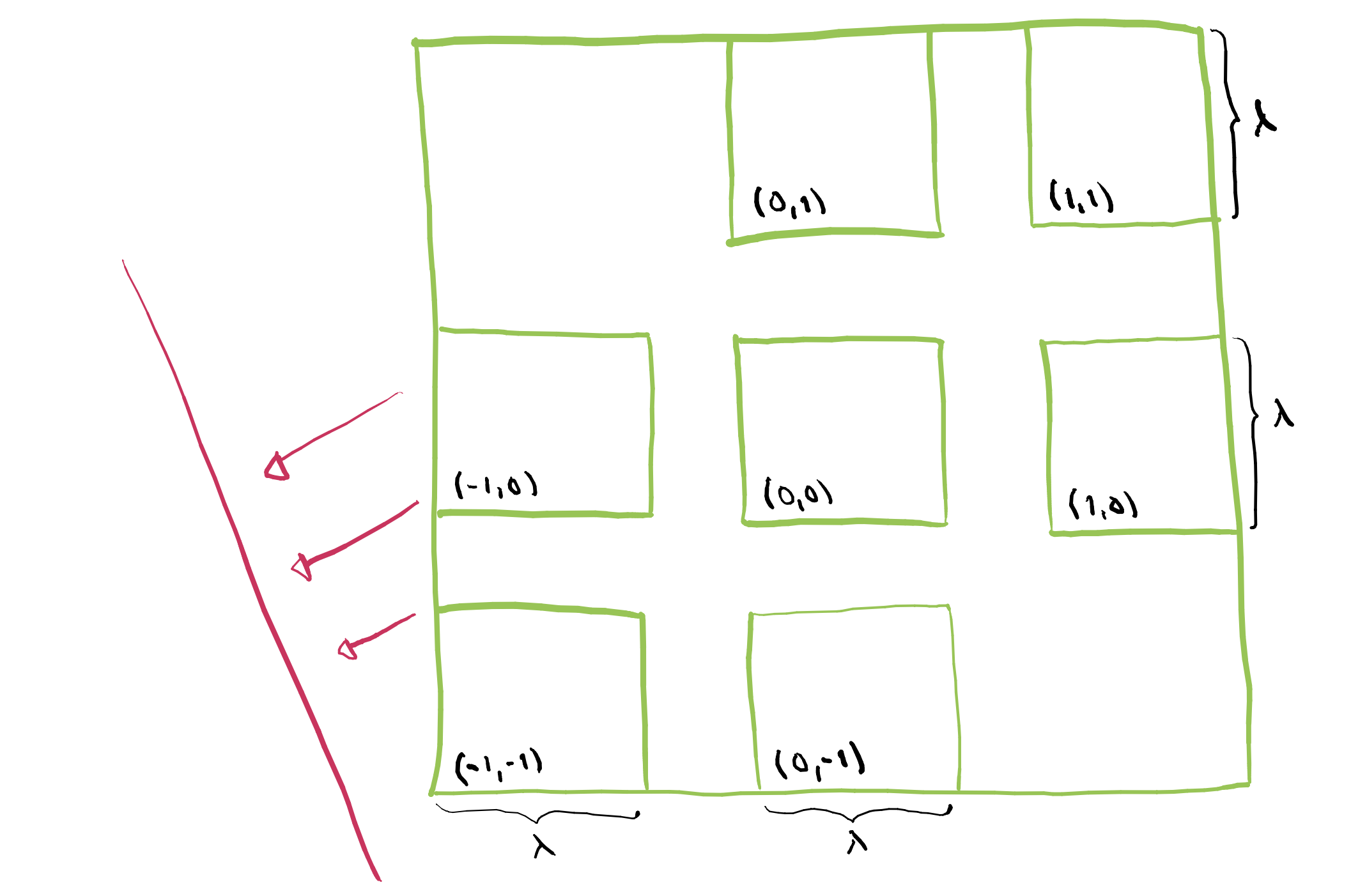
Lemma 8 thus transforms the problem to a study of non-linear projections of the planar self-similar set \(K_\lambda\) associated to \((S_{(i,j)}^\lambda)\): The rest of the proof is a rather standard transversality argument. The goal is to find a region of \(\lambda\)’s where the following holds:

Lemma 9. There exists \(\delta>0\) such that for every \(\lambda_0\) in this region and “many” finite sequences \(\mathtt{k} \ne \mathtt{l}\), we have

\[\delta < \frac{\mathrm{d}}{\mathrm{d}\lambda}\Bigl(\mathrm{proj}(S_{(\mathtt{i},\mathtt{j})}^\lambda(0,0)) - \mathrm{proj}(S_{(\mathtt{k},\mathtt{l})}^\lambda(0,0))\Bigr)\Big|_{\lambda=\lambda_0} < \delta^{-1}.\]

Furthermore, the projection of \(K_{\lambda_0}\) contains an interval for every \(\lambda_0\) in this region.

Lemma 9 is then used to show the existence of intervals of \(\lambda\) in which \(|t - \mathrm{proj}(S_{\beta(\mathtt{i},\mathtt{j})}^\lambda(0,0))|\) is as small as we wish but not zero. In fact, we perform a Moran construction with these intervals and get uncountably many \(\lambda\)’s.

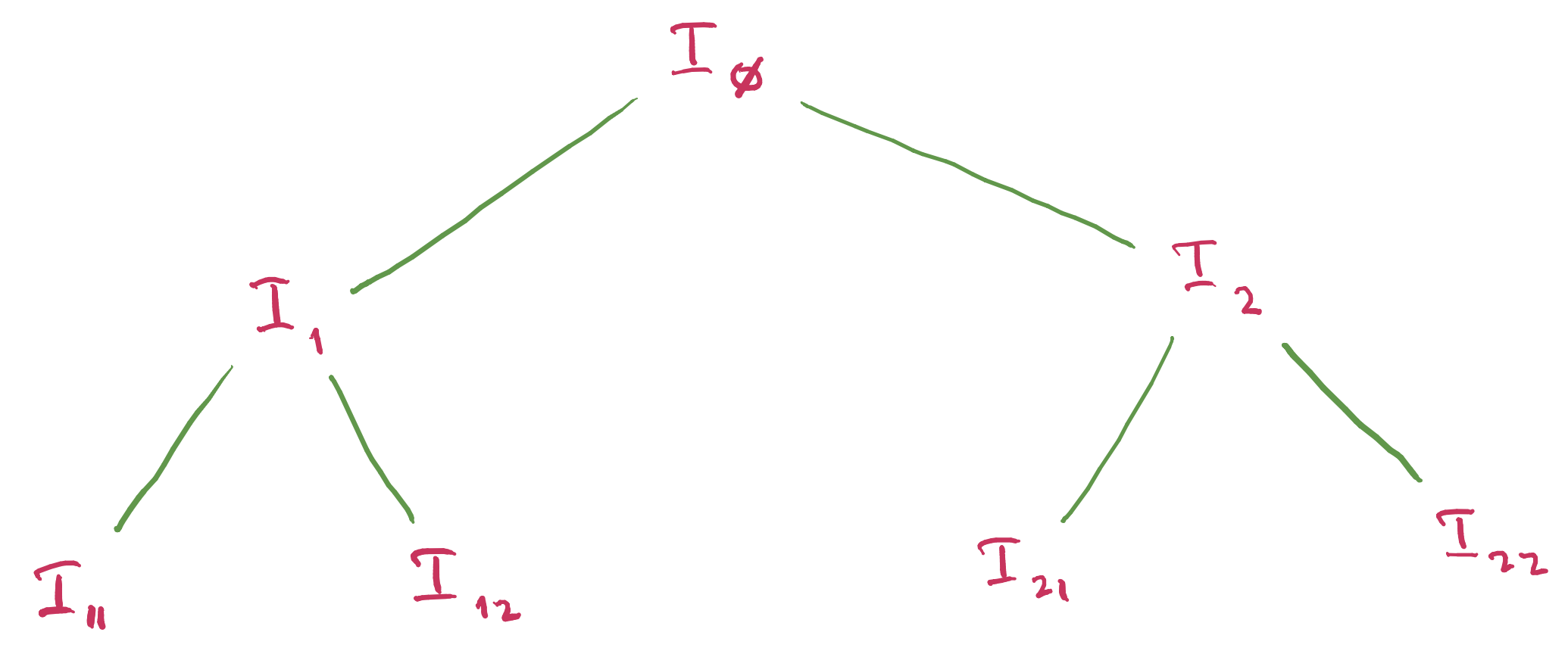
For each \(\lambda\) in this Cantor set, the associated translation vector \(t\) is obtained as \(\lim_{n\to\infty} \mathrm{proj}(S_{(\mathtt{i}|_n,\mathtt{j}|_n)}^\lambda(0,0))\). To show that these \((\lambda,t)\)’s belong to \(\mathcal{C}\) relies on how the construction intervals in the Cantor set were chosen and, of course, Lemma 8. If there is such \((\lambda,t)\) that belongs to \(\mathcal{E}\), then it is easy to see that \(t\) is not obtained as a limit, but as \(\mathrm{proj}(S_{(\mathtt{i},\mathtt{j})}^\lambda(0,0))\) with some finite sequence \((\mathtt{i},\mathtt{j})\). The construction of the Cantor set can be done so that this is a contradiction. Therefore these \((\lambda,t)\)’s do not belong to \(\mathcal{E}\). ■